Test: Congruence Criteria- SSS And RHS - Class 9 MCQ
10 Questions MCQ Test Mathematics (Maths) Class 9 - Test: Congruence Criteria- SSS And RHS
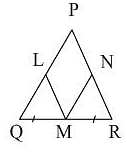
In isosceles ΔPQR, PQ = PR, M is the mid point of QR. LM ⊥ PQ, MN ⊥ PR. By which criterion of congruency is ΔQLM 0 ≅ ΔMNR.
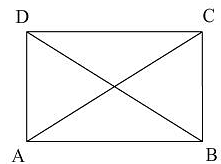
ABCD is a parallelogram, if the two diagonals are equal, then by what criterion are the triangles ABD and ABC congruent
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In ΔABC and ΔPBC, AB = BP and AC = PC. Can you say whether the triangles are congruent to each other or not:
In the given figure, AB = PQ, BC = QR and the median AD is equal to the median PM of the other triangle PQR, then ΔABD is congruent ΔPQM by the criterion
Two equilateral triangles are congruent when:
In the following figure, if PQR ≅ ABC, then
In the following figure, PT is the bisector of ___________.
PQRS is a parallelogram, if the two diagonals are equal, then the measure of PQR is:
Which of the following sets of conditions does not guarantee that two triangles are congruent?
|
44 videos|412 docs|54 tests
|
|
44 videos|412 docs|54 tests
|

















