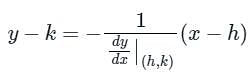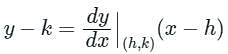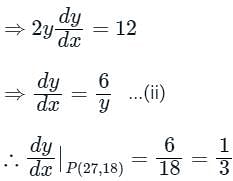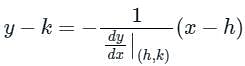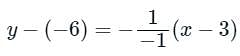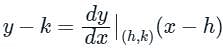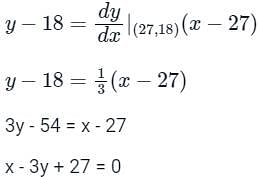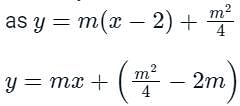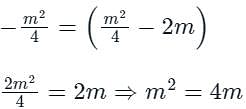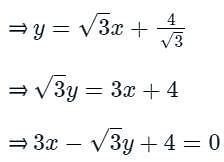Test: Equation of Parabola - Grade 12 MCQ
10 Questions MCQ Test Mathematics for Grade 12 - Test: Equation of Parabola
If a normal to the parabola y2 = 12x at A (3, - 6) cuts the parabola again at P, then the equation of the tangent at P is
The equation of common tangent to the parabola y = x2 and y = -(x - 2)2 is.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Comprehension:
Consider the following for the next three (03) items that follow:
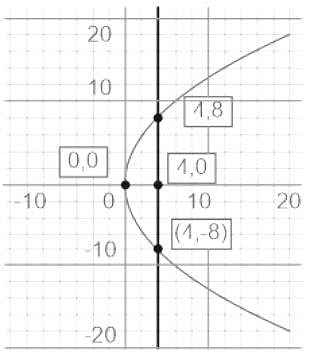
The two ends of the latus rectum of a parabola are (4, -8) and (4, 8)
The equation of directrix of the parabola is.
Consider the following for the next three (03) items that follow:
The two ends of the latus rectum of a parabola are (4, -8) and (4, 8)
The equation of directrix of the parabola is.
Comprehension: Consider the following for the next three (03) items that follow:
The two ends of the latus rectum of a parabola are (4, -8) and (4, 8)
The equation of the tangent to the parabola inclined at an angle of 60o to x-axis is.
Comprehension: Consider the following for the next three (03) items that follow:
The two ends of the latus rectum of a parabola are (4, -8) and (4, 8)
Find the equation of the parabola.
If the parabola has focus is (5, 0) and vertex is (3, 0) find its equation.
Find the equation of the parabola with vertex at (0, 0) and focus at (0, 4).
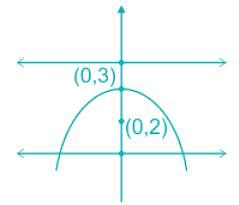
If the points (0, 3) and (0, 2) are respectively the vertex and focus of a parabola, then the equation of the parabola is
Find an equation of parabola has focus is (6, 0) and vertex is (4, 0)
If the parabola has focus is (4, 0) and vertex is (2, 0) find its equation.
|
175 videos|148 docs|98 tests
|
|
175 videos|148 docs|98 tests
|