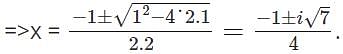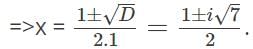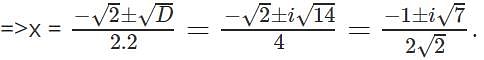Test: Quadratic Equations - 2 - Grade 12 MCQ
15 Questions MCQ Test Mathematics for Grade 12 - Test: Quadratic Equations - 2
Roots of a quadratic equation are real when discriminant is ______________
Roots of a quadratic equation are imaginary when discriminant is ______________
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
What will be the product of b * c if the equations x2 + bx + c = 0 and x2 + 3x + 3 = 0 have one common root?
If acosθ + bsinθ = c have roots α and β. Then, what will be the value of sinα + sinβ?
If acosθ + bsinθ = c have roots α and β. Then, what will be the value of sinα * sinβ ?
If x2 + ax + b = 0 and x2 + bx + a = 0 have exactly 1 common root then what is the value of (a + b)?
If, α and β are the roots of the equation 2x2 – 3x – 6 = 0, then what is the equation whose roots are α2 + 2 and β2 + 2?
If p and q are the roots of the equation x2 + px + q =0 then, what are the values of p and q?
If x2 + px + 1 = 0 and (a – b)x2 + (b – c)x + (c – a) = 0 have both roots common, then what is the form of a, b, c?
What will be the sum of b + c if the equations x2 + bx + c = 0 and x2 + 3x + 3 = 0 have one common root?
If |z1| = 4, |z2| = 3, then what is the value of |z1 + z2 + 3 + 4i|?
|
175 videos|148 docs|98 tests
|
|
175 videos|148 docs|98 tests
|


 . For real roots, radical must be non-negative i.e. discriminant should be greater than or equal to zero.
. For real roots, radical must be non-negative i.e. discriminant should be greater than or equal to zero.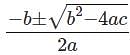 . For imaginary roots, radical is negative i.e. discriminant should be less than zero.
. For imaginary roots, radical is negative i.e. discriminant should be less than zero.