JEE Exam > JEE Tests > Mathematics (Maths) for JEE Main & Advanced > Test: Introduction To Functions - JEE MCQ
Test: Introduction To Functions - JEE MCQ
Test Description
15 Questions MCQ Test Mathematics (Maths) for JEE Main & Advanced - Test: Introduction To Functions
Test: Introduction To Functions for JEE 2024 is part of Mathematics (Maths) for JEE Main & Advanced preparation. The Test: Introduction To Functions questions and answers have been
prepared according to the JEE exam syllabus.The Test: Introduction To Functions MCQs are made for JEE 2024 Exam. Find important
definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Introduction To Functions below.
Solutions of Test: Introduction To Functions questions in English are available as part of our Mathematics (Maths) for JEE Main & Advanced for JEE & Test: Introduction To Functions solutions in
Hindi for Mathematics (Maths) for JEE Main & Advanced course. Download more important topics, notes, lectures and mock
test series for JEE Exam by signing up for free. Attempt Test: Introduction To Functions | 15 questions in 15 minutes | Mock test for JEE preparation | Free important questions MCQ to study Mathematics (Maths) for JEE Main & Advanced for JEE Exam | Download free PDF with solutions
Test: Introduction To Functions - Question 1
If y is expressed in terms of a variable x as Y = ƒ(x), then y is called
Detailed Solution for Test: Introduction To Functions - Question 1
Test: Introduction To Functions - Question 2
Let f : R → R defined as f(x) = x be an identity function. Then
Detailed Solution for Test: Introduction To Functions - Question 2
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Test: Introduction To Functions - Question 3
Let A = {1, 2, 3} and B = {5, 6, 7, 8, 9} and let f(x) = {(1, 8), (2, 7), (3, 6)} then f is
Detailed Solution for Test: Introduction To Functions - Question 3
Detailed Solution for Test: Introduction To Functions - Question 4
Test: Introduction To Functions - Question 5
Let f : N →N be defined by 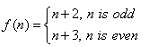 for all n ∈ N.
for all n ∈ N.
Then, the function f is
Detailed Solution for Test: Introduction To Functions - Question 5
Detailed Solution for Test: Introduction To Functions - Question 6
Detailed Solution for Test: Introduction To Functions - Question 7
Detailed Solution for Test: Introduction To Functions - Question 8
Detailed Solution for Test: Introduction To Functions - Question 9
Test: Introduction To Functions - Question 10
A function f: X → Y is surjective if and only if
Detailed Solution for Test: Introduction To Functions - Question 10
Test: Introduction To Functions - Question 11
The range of function f : R → R defined by f(x) = x2 is
Detailed Solution for Test: Introduction To Functions - Question 11
Test: Introduction To Functions - Question 12
Let f : R → R defined as f(x) = 5 be a constant function. Then
Detailed Solution for Test: Introduction To Functions - Question 12
Detailed Solution for Test: Introduction To Functions - Question 13
Test: Introduction To Functions - Question 14
Let f: {1, 2, 3} → {1, 2, 3} be an onto function. Then, f is
Detailed Solution for Test: Introduction To Functions - Question 14
Detailed Solution for Test: Introduction To Functions - Question 15
|
209 videos|443 docs|143 tests
|
Information about Test: Introduction To Functions Page
In this test you can find the Exam questions for Test: Introduction To Functions solved & explained in the simplest way possible.
Besides giving Questions and answers for Test: Introduction To Functions, EduRev gives you an ample number of Online tests for practice
|
209 videos|443 docs|143 tests
|
Download as PDF



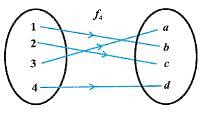
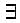 x in R such that f(x) = y.)
x in R such that f(x) = y.)














