Test: Absolute Equations- 1 - GMAT MCQ
15 Questions MCQ Test Quantitative for GMAT - Test: Absolute Equations- 1
Select the correct algebraic expression for the following number line representation:

What is the value of x?
(1) |2x + 3| = 4
(2) |4x – 4| = 2
Select the correct algebraic expression for the following number line representation:
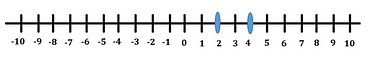
Select the correct algebraic expression for the following number line representation:
If x is a positive integer and |6 – 3x| = 9, what is the value of x?
If -|x+1| = b, where b is a non-zero integer, which of the following statements must be true?
I. b < 0
II. x < -b
III. x > b
Which of the following inequalities is an algebraic expression for the shaded part of the number line above?

If |x| > 6, which of the following expressions must be correct?
1.x < 6
II.–x < 6
III. x < -6 OR x > 6
Which of the following inequalities is an algebraic expression for the shaded part of the number line above?
If x is an integer where 2 -|x – 3| < 2, how many values of x are possible?
If x is a positive number and |-4x + 8| ≥ 2, which of the following statements is correct?
If |-1-x| ≤ 3, where x is a positive integer, what is the smallest possible value of x?
If x > 0, how many integer values of (x, y) will satisfy the equation 5x + 4|y| = 55?
|
115 videos|106 docs|113 tests
|


















