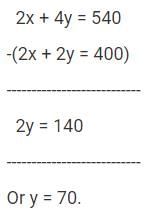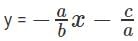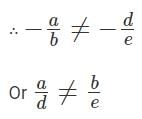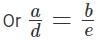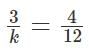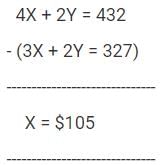All Courses
Get the App Signup / Login
Sign in Open App
GMAT Exam  >  GMAT Tests  >  Quantitative for GMAT  >  Test: Basic Algebra - GMAT MCQ

Test: Basic Algebra - GMAT MCQ


Test Description

10 Questions MCQ Test Quantitative for GMAT - Test: Basic Algebra

Test: Basic Algebra for GMAT 2024 is part of Quantitative for GMAT preparation. The Test: Basic Algebra questions and answers have been prepared according to the GMAT exam syllabus.The Test: Basic Algebra MCQs are made for GMAT 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Basic Algebra below.
Solutions of Test: Basic Algebra questions in English are available as part of our Quantitative for GMAT for GMAT & Test: Basic Algebra solutions in Hindi for Quantitative for GMAT course. Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free. Attempt Test: Basic Algebra | 10 questions in 20 minutes | Mock test for GMAT preparation | Free important questions MCQ to study Quantitative for GMAT for GMAT Exam | Download free PDF with solutions
Test: Basic Algebra - Question 1
Save

A poultry farm has only chickens and pigs. When the manager of the poultry counted the heads of the stock in the farm, the number totaled up to 200. However, when the number of legs was counted, the number totaled up to 540. How many more chickens were there in the farm? Note: In the farm, each pig had 4 legs and each chicken had 2 legs.

Detailed Solution for Test: Basic Algebra - Question 1
  • Step 1 : Assign Variables and Frame Equations
  • Let the number of chickens in the farm be 'x'.
  • Let the number of pigs in the farm be 'y'.
  • Each pig or each chicken has one head.
  • Therefore, number of heads will be the same as the sum of the chickens and pigs in the farm.
  • The count of the heads in the farm is 200. So, the sum of the number of chickens and pigs is 200.
  • So, x + y = 200 .... (1)
  • Each chicken has 2 legs and each pig has 4 legs
  • 'x' chickens will therefore, have 2x legs and 'y' pigs will have 4y legs.
  • The count of the legs in the farm is 540. So, the sum of the number of legs of chickens and the number of legs of pigs is 540.
  • Therefore, 2x + 4y = 540 .... (2)
  • Step 2 of solving this Linear Equations Question: Solve the system of linear equations
  • Multiply equation (1) by 2. We get 2x + 2y = 400 .... (3)
  • Subtract equation (3) from equation (2).
  • Substitute 'y' as 70 in equation (1). 
  • 70 + y = 200. So, x = 130
  • 'x' is the number of chickens in the farm. 'y' is the number of pigs in the farm. So, the farm has 130 chickens and 70 pigs.
  • Note:The question is "How many more chickens were there in the farm?"
  • The farm has 130 chickens and 70 pigs. So, the farm has (130 - 70) = 60 more chickens
Test: Basic Algebra - Question 2
Save

Three years back, a father was 24 years older than his son. At present the father is 5 times as old as the son. How old will the son be three years from now?

Detailed Solution for Test: Basic Algebra - Question 2
  • Let the age of the son 3 years back be 'x' years.
  • Information 1: Three years back, a father was 24 years older than his son. 
  • Therefore, the age of the father 3 years back was (x + 24).
  • If the age of the son 3 years back was 'x' years, the present age of the son is x + 3.
  • Present age of father = x + 24 + 3
  • Information 2: The father is at present 5 times as old as the son.
  • i.e., (x + 24 + 3) = 5(x + 3)
  • Or x + 27 = 5x + 15
  • Or 4x = 12 or x = 3.
  • x was the age of the son 3 years back.
  • Therefore, the son was 3 years old 3 years back.
  • If the son was 3 years old, 3 years back, the son is 6 years old now.
  • Hence, he will be 9 years old three years from now.
  • Choice D is the correct answer.
1 Crore+ students have signed up on EduRev. Have you? Download the App
Test: Basic Algebra - Question 3
Save

For what values of 'k' will the pair of equations 3x + 4y = 12 and kx + 12y = 30 NOT have a unique solution?

Detailed Solution for Test: Basic Algebra - Question 3
  • A system of linear equations ax + by + c = 0 and dx + ey + g = 0 will have a unique solution if the two lines represented by the equations ax + by + c = 0 and dx + ey + g = 0 intersect at a point.
    i.e., if the two lines are neither parallel nor coincident.
  • Essentially, the slopes of the two lines should be different.
  • What does that translate into?
  • ax + by + c = 0 and dx + ey + g = 0 will intersect at one point if their slopes are different.
  • Express both the equations in the standardized y = mx + c format, where 'm' is the slope of the line and 'c' is the y-intercept.
  • ax + by + c = 0 can be written as 
  • And dx + ey + g = 0 can be written as
  • Slope of the first line is -a/b and that of the second line is -d/e
  • For a unique solution, the slopes of the lines should be different.
  • Condition for the equations to NOT have a unique solution
  • The slopes should be equal
  • Apply the condition in the given equations to find k
  • In the question given above, a = 3, b = 4, d = k and e = 12.
  • Therefore,
  • Or 'k' should be equal to 9 for the system of linear equations to NOT have a unique solution.
  • When k = 9, the system of equations will represent a pair of parallel lines (their y-intercepts are different).
  • So, there will be NO solution to this system of linear equations in two variables.
  • Choice A is the correct answer.
Test: Basic Algebra - Question 4
Save

The basic one-way air fare for a child aged between 3 and 10 years costs half the regular fare for an adult plus a reservation charge that is the same on the child's ticket as on the adult's ticket. One reserved ticket for an adult costs $216 and the cost of a reserved ticket for an adult and a child (aged between 3 and 10) costs $327. What is the basic fare for the journey for an adult?
Detailed Solution for Test: Basic Algebra - Question 4
  • Step 1 : Assign variables and frame equations
  • Let the basic fare for the child be $X.
  • Information 1: Basic one-way air fare of a child costs half the regular fare for an adult.
  • Therefore, the basic fare for an adult = 2(basic one-way airfare for a child) = $2X.
  • Information 2: Reservation charge is the same on the child's ticket as on the adult's ticket.
  • Let the reservation charge per ticket be $Y
  • A child's ticket will cost (Basic fare + Reservation charges) = X + Y
  • Hence, an adult ticket will cost (Basic fare + Reservation charges) = 2X + Y.
  • Information 3: One reserved ticket for an adult costs $216. So, 2X + Y = $216 .... (1)
  • Information 4: The cost of a reserved ticket for an adult and a child (aged between 3 and 10) is $327.
  • So, the ticket for an adult and a child will cost (2X + Y) + (X + Y) = 3X + 2Y = $327 .... (2)
  • Step 2 Solve the simultaneous equations and determine basic fare for an adult.
  • Multiply equation (1) by 2: 4X + 2Y = 432 .... (3)
  • Subtract equation (2) from equation (3):
  • The basic fare of an adult ticket = 2X = 2*105 = $210
  • Choice C is the correct answer.
Test: Basic Algebra - Question 5
Save

A children's gift store sells gift certificates in denominations of $3 and $5. The store sold 'm' $3 certificates and 'n' $5 certificates worth $93 on a Saturday afternoon. If 'm' and 'n' are natural numbers, how many different values can 'm' take?
Detailed Solution for Test: Basic Algebra - Question 5
  • Step 1: Understand Key Data
  • The total value of all certificates sold = $93.
  • Certificates sold were in denominations of $3 and $5.
  • Both 'm' and 'n' are natural numbers.
  • Approach to solve this GMAT Algebra Word Problem
  • The value of all certificates sold, 93 is divisible by 3.
  • So, a maximum of 31 $3 certificates and no $5 certificates could have been sold.
  • However, the question states that both 'm' and 'n' are natural numbers.
  • Hence, at least 1 $5 certificate should have been sold.
  • Let us reduce the number of $3 certificates from the theoretical maximum count of 31 by say 'x' and correspondingly increase $5 certificates by 'y'.
  • Evidently, 3x = 5y because the value of $3 certificates reduced should be the same as the value of $5 certificates increased.
  • It means that x has to be a multiple of 5 and y has to be a multiple of 3.
  • Or $3 certificates reduce in steps of 5 certificates.
  • Step 2 of solving this GMAT Algebra Question: List down possible values for 'm' and 'n'
  • The following combinations are possible.
  • m = 26, n = 3
  • m = 21, n = 6
  • m = 16, n = 9
  • m = 11, n = 12
  • m = 6, n = 15
  • m = 1, n = 18
  • Hence, m can take 6 values.
  • Choice C is the correct answer.
Test: Basic Algebra - Question 6
Save

What is the highest integral value of 'k' for which the quadratic equation x2 - 6x + k = 0 will have two real and distinct roots?
Detailed Solution for Test: Basic Algebra - Question 6
  • Step 1: Nature of Roots of Quadratic Equation Theory
  • D is called the Discriminant of a quadratic equation.
  • D = b2 - 4ac for quadratic equations of the form ax2 + bx + c = 0.
  • If D > 0, roots of such quadratic equations are Real and Distinct
  • If D = 0, roots of such quadratic equations are Real and Equal
  • If D < 0, roots of such quadratic equations are Imaginary. i.e., such quadratic equations will NOT have real roots.
  • Step 2:Compute maximum value of k that will make the discriminant of the quadratic equation positive
  • The given quadratic equation is x2 - 6x + k = 0.
  • In this equation, a = 1, b = -6 and c = k
  • The value of the discriminant, D = 62 - 4 * 1 * k
  • We have compute values of 'k' for which D > 0.
  • i.e., 36 – 4k > 0
  • Or 36 > 4k or k < 9.
  • If k < 9, the highest integer value that k can take is 8.
  • Choice D is the correct answer.
Test: Basic Algebra - Question 7
Save

 If one of the roots of the quadratic equation x2 + mx + 24 = 0 is 1.5, then what is the value of m?
Detailed Solution for Test: Basic Algebra - Question 7
  • If 1.5 is a root of the quadratic equation, substituting x = 1.5 in the equation will satisfy the equation.
  • The given quadratic equation is x2 + mx + 24 = 0
  • Substitute x = 1.5 in the above equation because 1.5 is a root of the equation.
  • (1.5)2 + 1.5m + 24 = 0
  • 2.25 + 1.5m + 24 = 0
  • 1.5m = -26.25 Or 
Test: Basic Algebra - Question 8
Save

For what value of 'm' will the quadratic equation x2 - mx + 4 = 0 have real and equal roots?
Detailed Solution for Test: Basic Algebra - Question 8
  • Step 1:Nature of Roots of Quadratic Equations Theory
  • D is the Discriminant in a quadratic equation.
  • D = b2 - 4ac for quadratic equations of the form ax2 + bx + c = 0.
  • If D > 0, roots are Real and Unique (Distinct and real roots).
  • If D = 0, roots are Real and Equal.
  • If D < 0, roots are Imaginary. The roots of such quadratic equations are NOT real.
  • The quadratic equation given in this question has real and equal roots. Therefore, its discriminant D = 0.
  • Step 2:Compute discriminant for the equation in terms of ‘m’ and find the value of ‘m’.
  • In the given equation x2 - mx + 4 = 0, a = 1, b = -m and c = 4.
  • Therefore, the discriminant b2 - 4ac = m2 - 4(4)(1) = m2 - 16.
  • The roots of the given equation are real and equal. 
  • Therefore, m2 - 16 = 0 or m2 = 16 or m = +4 or m = -4.
  • Choice (D) is the answer to this quadratic equations question.
Test: Basic Algebra - Question 9
Save

y = x2 + bx + 256 cuts the x axis at (h, 0) and (k, 0). If h and k are integers, what is the least value of b?
Detailed Solution for Test: Basic Algebra - Question 9
  • Step 1:Understand the equation and the points (h, 0) and (k, 0)
  • The given equation is a quadratic equation. A quadratic equation when plotted on a graph sheet (x - y plane) will result in a parabola.
  • The roots of the quadratic equation are computed by equating the quadratic expression to 0. i.e., the roots are the values that 'x' take when y = 0
  • So, the roots of the quadratic equation are the points where the parabola cuts the x-axis.
  • The question mentions that the curve described by the equation cuts the x-axis at (h, 0) and (k, 0). So, h and k are the roots of the quadratic equation.
  • For quadratic equations of the form ax2 + bx + c = 0, the sum of the roots = -b/a
  • The sum of the roots of this equation is 
  • Note : Higher the value of 'b', i.e., higher the sum of the roots of this quadratic equation, lower the value of b.
  • For quadratic equations of the form ax2 + bx + c = 0, the product of roots = c/a
  • Therefore, the product of the roots of this equation = 256/1 = 256
  • i.e., h * k = 256 h and k are both integers.
  • So, h and k are both integral factors of 256.
  • Step 2 : List possible values of h and k and find the least value of ‘b’
  • This is the step in which number properties kicks in. 256 can be expressed as product of two numbers in the following ways:
  • 1 x 256
  • 2 x 128
  • 4 x 64
  • 8 x 32
  • 16 x 16
  • The sum of the roots is maximum when the roots are 1 and 256 and the maximum sum is 1 + 256 = 257.
  • ∴ The least value possible for b is -257.
  • Choice D is the correct answer.
Test: Basic Algebra - Question 10
Save

The cost C and revenue R of a product depend on the number of units x produced. The equations are:

  • C=5000+20x
  • R=50x

Find the number of units x that must be produced for the company to break even (i.e., where revenue equals cost).
Detailed Solution for Test: Basic Algebra - Question 10
  • To find the break-even point, set C=R
  • 5000+20x=50x
  • Rearrange terms:
  • 5000=30x
  • hence, x = 166.66 = 167 units.
115 videos|106 docs|113 tests
Join Course
Information about Test: Basic Algebra Page
In this test you can find the Exam questions for Test: Basic Algebra solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Basic Algebra, EduRev gives you an ample number of Online tests for practice

Top Courses for GMAT

115 videos|106 docs|113 tests
Join Course
Download as PDF

Top Courses for GMAT

Important Questions for Basic Algebra

Find all the important questions for Basic Algebra at EduRev.Get fully prepared for Basic Algebra with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Basic Algebra syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Basic Algebra resources.

Basic Algebra MCQs with Answers

Prepare for the Basic Algebra within the GMAT exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Basic Algebra Quantitative for GMAT

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Basic Algebra with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup