Test: Calculations, Exponents And Basic Algebra - GMAT MCQ
10 Questions MCQ Test Quantitative for GMAT - Test: Calculations, Exponents And Basic Algebra
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A, B, C, D, E, F, G, and H are all integers, listed in order of increasing size. When these numbers are arranged on a number line, the distance between any two consecutive numbers is constant. If G and H are equal to 512 and 513, respectively, what is the value of A?
The three-digit positive integer x has the hundreds, tens, and units digits of a, b, and c, respectively. The three-digit positive integer y has the hundreds, tens, and units digits of k, l , and m, respectively. If (2a)(3b)(5c) = 12(2k)(3l)(5m), what is the value of x – y?
If 274x + 2 × 162-2x × 36x × 96 – 2x = 1, then what is the value of x?
If (22x+1)(32y-1) = 8x27y, then x + y =
x2 + bx + 72 = 0 has two distinct integer roots; how many values are possible for 'b'?
If x > 0, how many integer values of (x, y) will satisfy the equation 5x + 4|y| = 55?
|
110 videos|110 docs|120 tests
|
|
110 videos|110 docs|120 tests
|


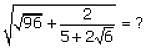 lies between:
lies between: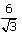 is simplified by multiplying by
is simplified by multiplying by 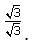
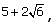 we multiply by the conjugate,
we multiply by the conjugate, 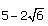 as follows:
as follows: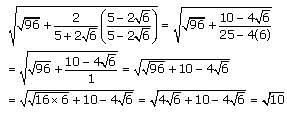
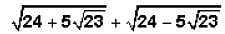 lies between:
lies between: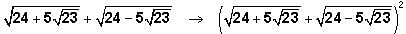
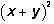 where
where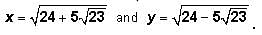
 This is one of the GMAT's favorite expressions.
This is one of the GMAT's favorite expressions.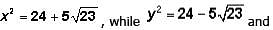
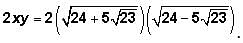
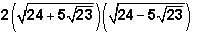 recall that
recall that 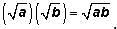
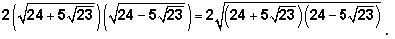
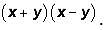 And recall that
And recall that 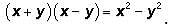 This is another one of the GMAT's favorite expressions. Returning to our expression:
This is another one of the GMAT's favorite expressions. Returning to our expression: 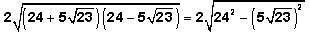
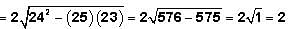
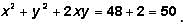
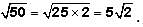


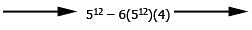

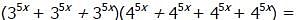
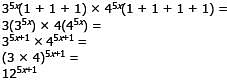
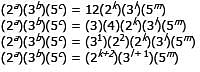
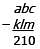
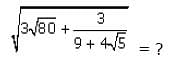

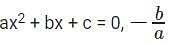 represents the sum of the roots of the quadratic equation and c/a
represents the sum of the roots of the quadratic equation and c/a 









