Test: Coordinate Geometry- 2

Given:

• Regular hexagon ABCDEF
  • This means, each interior angle of this hexagon will measure 120^o
    • (Here’s how you can calculate this: Measure of each angle of a regular n-sided polygon =  
    • So, for a regular hexagon (n  =6), each interior angle =
    • Let each side of this hexagon measure a units

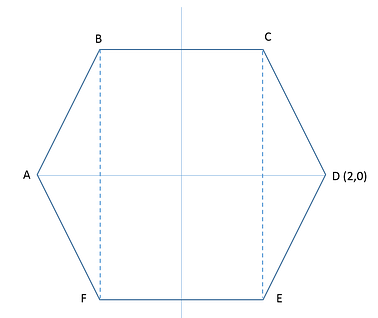
    • Hexagon ABCDEF is symmetrical about the x-axis and the y-axis.

      • This means, the center of the coordinate plane O(0,0) lies at the exact center of the hexagon
    • Point D(2,0)

    • To find: ar(Rectangle BCEF

      Approach:

    • We need to find the value of Ar(Rectangle BCEF)
      • Note that since the origin lies at the exact center of the hexagon, and hence also at the center of rectangle BCEF, it will divide rectangle BCEF into 4 smaller and identical rectangles.
      • Let’s label one of these rectangles as OGCH
      • So, Ar(Rectangle BCEF) = 4*ar(Rectangle OGCH)

2. ar(Rectangle OGCH)= CG*CH

• Since the hexagon is symmetrical about the x-axis,

• And, since the hexagon is symmetrical about the y-axis,

• So, if we can find CG and a, we can answer the question.

. Now, OG + GD = OD

• We know the value of OD.
• Using trigonometric ratios in right triangle CGD, we can express DG in terms of hypotenuse a (Note that the hypotenuse of this triangle is the side of regular hexagon ABCDEF, and so, is equal to a units)
• We already know the value of OG in terms of a
• So, from this equation, we can find the value of a

4. Also, in right triangle CGD, using trigonometric ratios, we can express CG in terms of hypotenuse a.

• So, once we know the value of a, we can find the value of CG as well

Working Out:

• Finding the value of a

• Finding the value of CG

Working towards the final answer

• Therefore, ar(Rectangle BCEF)
• Looking at the answer choices, we see that the correct answer is Option D

Steps 1 & 2: Understand Question and Draw Inferences

• Lines L₁ and L₂ intersect at point C

To Find:

• If lines L₁ and L₂ are perpendicular?
  • Let’s assume the slopes of lines L₁ and L₂ be m₁ and m₂
  • So, we need to find if m₁ * m₂  = -1?

Step 3: Analyze Statement 1 independently

(1)  Statement 1 states that: "The product of the slopes of lines L₁ and L₂ is at a distance of 1 unit from 0 on the number line."

• Numbers that are at a distance of 1 unit from 0 on the number line:
  • 0 + 1 = 1 and
  • 0 – 1 = -1
• So, as per Statement 1, Product of slopes, that is,= m₁ * m₂  = 1 or -1
• If m₁ * m₂  = 1, lines L₁ and L₂ are not perpendicular to each other
• If m₁ * m₂  = -1, lines L₁ and L₂ are perpendicular to each other
• Thus, statement 1 is not sufficient to answer.

Step 4: Analyze Statement 2 independently

(2)  Statement 2 states that: "Lines x = 0 and y = 0 are the perpendicular bisectors of lines L₁ and L₂ respectively."

• As x= 0 is the perpendicular bisector of line L_1, L₁ is perpendicular to line x= 0 i.e. L₁ is the y –axis
• As y = 0 is the perpendicular bisector of line L_2, L₂ is perpendicular to line y = 0 i.e. L₂ is the x –axis

• Since x axis and y-axis are perpendicular to each other, lines L₁ and L₂ will also be perpendicular to each other.
• Hence, Statement 2 is sufficient to answer the question

Step 5: Analyze Both Statements Together (if needed)

As we have got a unique answer from step-4, this step is not required.

• Thus the correct answer is Option B.

Steps 1 & 2: Understand Question and Draw Inferences

Given: Rectangle ABCD in the xy-plane

• Since AB is parallel to the x-axis,
  • Points A and B will have the same y-coordinates
  • Since side CD of the rectangle will be parallel to side AB, points C and D too will have the same y-coordinates
• Since AD is parallel to the y-axis,
  • Points A and D will have the same x-coordinates
  • Since side BC of the rectangle will be parallel to side AD, points B and C too will have the same x-coordinates

To find: Coordinates of point D

Step 3: Analyze Statement 1 independently

Statement 1 says that ‘The coordinates of point A are (2, 3)’

• This means, the x-coordinate of point D is 2
• However, since we do not know the y-coordinate of point D, Statement 1 alone is not sufficient

Step 4: Analyze Statement 2 independently

Statement 2 says that ‘The coordinates of point C are (4, 8)’

• This means, the y-coordinate of point D is 8
• However, since we do not know the x-coordinate of point D, Statement 2 alone is not sufficient

Step 5: Analyze Both Statements Together (if needed)

• From Statement 1, the x- coordinate of point D is 2
• From Statement 2, the y-coordinate of point D is 8
• So, the coordinates of point D are (2,8)

Thus, by combining the 2 statements, we do get a unique answer

Answer: Option C

Given:

• The given information corresponds to the following diagram:

In ΔABC

• Length of side AB = 5 – (-1) = 6 units
• Side AB is the diameter of the circle
  • So, ∠ACB is the angle in a semicircle
  • Therefore, ∠ABC = 90⁰
  • Also, Radius of circle = 6/2 = 3 units
  • So, OB = 3 units, where O is the center of the circle
  • The coordinate of point O will be (2,0)

• Area of ΔABC = 6√2 square units

To find: Possible coordinates of point C

Approach and Working:

• We know the area of ΔABC.
• As per the formula, the area of this triangle = ½ * base * height = ½ * AB * the perpendicular dropped from C on AB.
• Now AB lies on the x-axis. So, what will be the length of the perpendicular dropped from C on AB ?
  • It will be equal to the y-coordinate of C.

• So, we can write:
  • ½ (AB)(y-coordinate of point C) = 6√2
  • ½* 6* (y-coordinate of point C) = 6√2
  • (y-coordinate of point C) = 2√2
• To find the x-coordinate of C, we can use the distance formula.
• The distance between the center and C is 3 units. Thus, we can write:
  • D = √[(x-2)² + (2√2 -0)²]
  • 3 = √[(x²-4x +4 + 8]
  • x² -4x +12 = 9
  • x² -4x + 3 = 0
  • (x-1)* (x-3) = 0
  • Therefore, x can be either 1 or 3.

• Looking at the answer choices, we see that only option B (1,2√2) satisfy.
• Thus, the correct answer is Option B.

Steps 1 & 2: Understand Question and Draw Inferences

• Circle C with center at (1, 2) and r = 5

To Find: Is line l a tangent to the circle?

• For a line l to be a tangent to the circle, the circle C and the line l should share exactly one common point, i.e. a point lying on circle C should also lie on the line l
  • For a point to lie on the circle C, the distance of the point from the center (1,2) should be exactly equal to radius of the circle i.e. 5 units.
• Assuming the coordinates of a point lying on the circle to be (x, y), we can write  

​​

• Using the same logic, if a point lies inside the circle, its distance from the center (1,2) should be less than 5 units.
• Assuming the coordinates of a point lying inside the circle to be(x,y), we can write  
• Similarly, if a point lies outside the circle, its distance from the center (1,2) should be greater than 5 units.
• Assuming the coordinates of a point lying outside the circle to be(x,y), we can write 

• • So, we can summarize the following:
    • A point (x, y) will lie inside the circle if x(x - 2) + y(y - 4) = 20
    • A point (x, y) will lie on the circle if x(x - 2) + y(y - 4) < 20
    • A point (x, y) will lie outside the circle if x(x - 2) + y(y - 4) > 20

Step 3: Analyze Statement 1 independently

1.Statement 1 states that: "Point A with coordinates (a, b) lies on line l such that a(a-2) +b(b-4) ≤ 20".

• As a(a-2) +b(b-4) ≤ 20, two cases may arise:
  • If a(a-2) +b(b-4) = 20, the point A would lie on the circle. However, we cannot say if the line L meets circle C at only point A or at two different points.(one of which is Point A)
  • If a(a-2) +b(b-4) < 20, point A would lie inside the circle. So, line l passes through the circle and hence is not a tangent to the circle C.
  • Thus, Statement 1 is Insufficient to answer.

Step 4: Analyze Statement 2 independently

2. Statement 2 states that "The x-intercept of line l is 10".

• The line l intersects the x- axis at point (10, 0)
• Refer the below diagram:
  • A line with x- intercept 10 may or may not be a tangent to the circle with center at (1,2)

• Thus, Statement 2 is also Insufficient to answer

Step 5: Analyze Both Statements Together (if needed)

• a(a-2) +b(b-4) ≤ 20
• x-intercept of line l is 10.
• Combination, of the two statements does not provide us with any extra information to answer the question.
• Hence, both the statement together are also Insufficient to answer.

Thus, the correct answer is Option E .

Steps 1 & 2: Understand Question and Draw Inferences

The given information can be represented visually as under:

We need to find if AB = BC, that is, if B is the mid-point of AC?

• From the figure, it is clear that the answer is YES only if:
  • The x-coordinate of B = (mid-point between the x-coordinates of points A and C) = mid-point between (2 and
  • AND, the y-coordinate of B = (mid-point between the y-coordinates of points A and C) = mid-point between
    • So, we see that the answer is YES if the coordinates of point B are (3, 2)
  • Now, we are given that point B lies on the line segment AC.
    • Since we know the coordinates of both points A and C, we can find the equation of line segment AC:
      • Starting with the general equation: y = mx + c, where m is the slope of the line and c is the y-intercept
      • Since this line passes through point A (2, 1), we can write: 1 = 2m + c . . . (1)
      • And, since this line passes through point C(4, 3), we can write: 3 = 4m + c .  . .(2)
      • (2) – (1): 2 = 2m
        • So, m = 1
      • From (1): 1 = 2 + c
        • So, c = -1
    • Therefore, the equation of line AC = y = x – 1
    • Since point B lies on line AC, it will satisfy this equation.
  • So, if we know either the x-coordinate or the y-coordinate of point B, we will be able to find the other coordinate of point B using the equation of the line.
  • Once we know both the x- and the y- coordinates of point B, the answer will be YES if these coordinates are (3, 2); else the answer will be NO
  • Thus, in order to answer the question, we only need to know either the x- or the y-coordinate of point B

Step 3: Analyze Statement 1 independently

Statement 1 says that ‘The x-coordinate of point B is 3’

• Since we know the x-coordinate of point B, using the equation of line AC (y = x – 1), we can find the y-coordinate of point B
• Therefore, we can answer if the coordinates of point B are (3,2) or not
• So, Statement 1 alone is sufficient to answer the question

Step 4: Analyze Statement 2 independently

Statement 2 says that ‘The y-coordinate of point B is 2’

• Since we know the y-coordinate of point B, using the equation of line AC (y = x – 1), we can find the x-coordinate of point B
• Therefore, we can answer if the coordinates of point B are (3,2) or not
• So, Statement 2 alone is sufficient to answer the question

Step 5: Analyze Both Statements Together (if needed)

Since we’ve already arrived at a unique answer in Steps 3 and 4, this step is not required

Hence, the correct answer is Option D.

Given

x²+ y² =25 

To Find: Percentage of points lying on the circle that satisfies xy ≥ 0?

Approach and Working

• x² + y² = 25
  • If we compare it with the distance formula:
    • ■   D² = [(xi - ^x2⁾² + (yi ^- y2)²]
    • ■   If (x₂, y₂) is considered as the origin, (x, y) as the other point
    • ■   We can write: (x-0)² + (y-0)² = 5²
    • ■   Thus, we are looking for all the points which are at a distance of 5 units from the origin.
  • o If we try to plot it on a graph, we will notice that
    • This equation represents all the points lying on a Circle C with center(0,0) and radius of 5 units.
• xy > 0, when the x and the y coordinates have the same signs, except for the case when either of x or y = 0
  • x and y coordinates have the same signs in the 1^st and the 3^rd quadrant. So, we need to find the percentage of points of circle C that lie in the 1^st and the 3^rd quadrant.
• A circle with center at origin will pass through all the 4 quadrants.
  •  So, if we find the arc length of the circle in the 1^st quadrant and the 3^rd quadrant, we can divide it by the total arc length of the circle (i.e. the circumference) to find the percentage of points satisfying the inequality xy > 0

• We can see from the figure above that by symmetry, arc length of the circle in each quadrant = 1/4th of its total circumference = ¼ * 2πr
• So, the total arc length present in the 1st and the 3rd quadrant = (¼ + ¼) *2πr = ½ *2πr
• Hence, 50% of the points that lie on the circle, satisfy the inequality xy ≥0
• And the correct answer is OPTION C

Given

• y +2x ≥ 3
• y –x ≥ -6
• Line perpendicular to x=0 and passing through origin
  • The equation x = 0 represents the y-axis
  • So, the given line is perpendicular to the y-axis and passes through the origin
  • Therefore, the given line is the x-axis

To Find: Area bounded by the region y +2x ≥ 3, y –x ≥ -6 and x-axis

Approach: 

1. For finding the area bounded by the region, we need to first draw the line segments y +2x = 3 and y – x = 6

2. Once we draw these line segment, we need to find the side of each line segment where the region specified in the question statement lies

• For finding the region, we will put the coordinates of the origin (0,0) in the inequality. If the inequality is satisfied, the region lies towards the side of the line containing the origin, else it lies on the opposite side of the line containing the origin.

3. Once we have the region, we will find the area of the region using the standard geometry formulas

Working out:

1. The line segment y +2x = 3 will intersect the y-axis at (3,0) and x-axis at 

• The region y +2x – 3 ≥ 0 will be satisfied by the region, which does not contain the origin, as putting (0,0) in the inequality does not satisfy the inequality.

2. Similarly, the line segment y-x ≥ 6 will intersect the y-axis at (-6,0) and x-axis at (6,0).

• The region y-x ≥ -6 will consist of the region, which contains the origin.

3. So, the vertex points of the region are ,(6,0) and (3, -3)

4. We know that area of a triangle = ½ * base * height

• Let’s consider the base as the x-axis, thus length of the base 
• Height of the triangle would be the magnitude of y-coordinate of point (3, -3) = 3

5.  Thus area of the triangle = 

Hence the correct answer is Option B.

Given

• The line intersects the y-axis at the point P
• The line  intersects the y-axis at the point R
• The lines  and 0
•  intersect at point Q,

To Find: ∠PQR = ?

Approach

• In order to answer this question, we first need to be able to draw ΔPQR in the coordinate plane.
  • Once we’ve drawn ΔPQR, we’ll be able to use trigonometric ratios to find the required angle
• In order to draw ΔPQR in the coordinate plane, we need to know the coordinates of points P, Q and R.

Working out

• Finding the coordinates of R
  • R is the point of intersection of line  with x = 0 (this is the equation of
    the y-axis)
    
  • Therefore, the coordinates of point R are (0, -1)

• Finding the coordinates of Q

​

• Thus, the coordinates of point Q are ( 

Drawing ΔPQR in the coordinate plane

• Now that we know the coordinates of P, Q and R, we can draw ΔPQR in the coordinate plane as under:

Finding ∠PQR
∠PQR = ∠PQO + ∠OQR

Step 1 & 2: Understand Question and Draw Inference

• Lines l and k intersect in quadrant I
• Lines l and k are not parallel to x or y –axis.
• Let the slopes of lines l and k be m and m respectively

To Find: Is m * m > 0?

• The answer to the question will be YES if slope of lines l and k are both positive or both negative
  • Lines with positive slopes can pass through:
    • Either quadrant I, III and IV or
    • Quadrant I, II and III or
    • Quadrant I, III through the origin
  • Here all the 3 types of lines pass through quadrant-I. So, all the 3 cases are possible.
    • We should also take note the positive-negative nature of x-intercepts and the y-intercepts of the lines above:

• Lines with negative slopes can pass through:
  • Quadrants II, III and IV or
  • Quadrant II, IV through the origin or
  • Quadrant II, I and IV
• Out of the above cases only one line passes through quadrant-I, the only possible case is a line passing through quadrants II, I and IV.
• Also note that for a line having a negative slope and passing through quadrant-I has a positive x-intercept as well as a positive y-intercept 

Step 3 : Analyze Statement 1 independent

(1) The product of the x-intercepts of the lines l and k is negative.

• We are given that the product of the x-intercepts of lines l and k is negative
  • Possible cases can be case-I, II and IV
  • For these cases we may have the product of slopes of lines l and k as negative or positive.

Insufficient to answer.

Step 4 : Analyze Statement 2 independent

(2) The product of the y-intercepts of the lines l and k is positive.

• We are given that product of the y-intercepts of lines l and k is positive
  • All the four cases are possible
  • For these cases we may have the product of slopes of lines l and k as negative or positive.

Insufficient to answer.

Step 5: Analyze Both Statements Together (if needed)

Combining both the statements, we can reject case-III, where slopes of both the lines is negative. Now, let’s evaluate the other cases one by one:

• Case-I and IV: Slopes of both the lines are positive
  • A line with a positive slope will have
    • A positive y-intercept and a negative x- intercept or
    • A negative y –intercept and a positive x- intercept
    • For product of y-intercepts of the line to be positive, both the lines should have a positive y-intercept(in this case the product of x-intercepts will also be positive) or negative yintercepts(
      in this case the product of x – intercept will be positive)
    • Thus it is not possible to have a case where the product of
      y-intercepts is positive and the product of x-intercepts of the
      line is negative.
    • Case Rejected

Case-II: Lines have opposite slopes

• A line with a positive slope will have
  • A positive y-intercept and a negative x- intercept or
  • A negative y –intercept and a positive x- intercept
• A line with a negative slope will have
  • A positive y-intercept and a positive x-intercept
• For product of y-intercepts to be positive and x-intercepts to be negative, the only possible case is when one of the line has positive slope and the other has negative slope.

Case Accepted: the product of Slope in such a case will be negetive

Thus, we have a unique answer. Sufficient to answer Answer: C

step 1 & 2: Understand Question and Draw Inference

To Find: If points A and B are equidistant from C (1, 0)?

Step 3 : Analyze Statement 1 independent

(1) Points A and B lie on circle R, which passes through origin and has a radius equal to 1.

• There can be various circles possible with radius = 1 and passing through origin. Refer the diagram:

• If points A and B lie on the circle with center at C(1, 0), points A and B will be equidistant from C
• For all the other cases, points A and B may not be equidistant from

Insufficient to answer

Step 4 : Analyze Statement 2 independent

(2) The bisector of the line segment AB passes through point C

• Following cases are possible:
  • If the bisector of the line segment AB is the perpendicular bisector, then all the points on the perpendicular bisector will be equidistant from A and B.

• If the bisector is not a perpendicular bisector then point C may or may not be equidistant from points A and B.
  • If point C lies on line AB as well as on the bisector of AB then, points A and B will be equidistant from C.
  • If point C lies on the bisector of AB then but not on AB, points A and B will not be equidistant from point C.

• Insufficient to answer

Step 5: Analyze Both Statements Together (if needed)

Both the statements combined does not give us any extra information to answer
the question.

Insufficient to answer
Answer: E

Given

Trapezium ABCD with AB on x-axis

• Coordinates of A = (0,0)
• x-coordinate of B =6
  • Coordinate of B (6,0)
• CD = AB – 2
• AD lies on the line y =x
  • Let’s assume the coordinate of point D (a, a)
• Ar(ABCD) = 5

To Find: Coordinates of point C?

Approach:

• As AB lies on x-axis and CD is parallel to AB, the y-coordinate of point C will be equal to y-coordinate of point D, i.e. a
• The x-coordinate of point C will be x-coordinate of point D + length of CD, i.e. (a + CD)
  • Now, we have expressed the coordinates of point C in terms of a and length of CD
• Now, we are given that the length of CD is 2 less than the length of AB. As we know the coordinates of points A and B, we can find the length of AB and hence the length of CD.
• So, we now need to find the value of a to find the coordinates of point C We know that area of trapezium ABCD = ½ * (AB + CD) * distance between AB and CD
  • As we are given the value of the area of the trapezium, AB and CD, we will get the distance between the parallel lines from the above equation.
  • Now, the distance between the parallel lines will be equal to the y-coordinate of point C. Thus, we will get the value of a from here.

Working out

• Length of AB = x-coordinate of point B – x coordinate of point A = 6 – 0 = 6 units
• Hence, length of CD = 6 – 2 = 4 units
• So, coordinate of point C = (a + CD, a) = (a+4, a)
• Area of trapezium ABCD = ½ *(AB+CD) * distance between AB and CD
  • As distance between AB and CD is equal to the y-coordinate of point C, we can write
  • Area if trapezium = 5 = ½ *(6+4) * (a)
  • Thus a = 1 and a+4 = 5
  • Hence, coordinate of point C (5, 1)
• Thus, the correct answer is Option C

• Circle R
  • Origin = (2, 3)
  • Radius = 5
  • Now, all the points that lie on the Circle R will be at a distance of 5

units (i.e. the radius) from the centre of the circle(2, 3)

To Find: The equation of the line that passes through the intersection point of Circle C and R?

Approach: 

• To find the equation of a line that passes through the intersection points of Circles C and R, we need to find two points that lie on the line.

• As the line passes through the two intersection points of the circles C and R, the equation of the line will satisfy these two intersection points.

• Also the two intersection points of the circles should satisfy the equation of all the points lying on both the circles.

• So, we can equate the equations of the points lying on circle C and R to find the equation of the line passing through the intersection points.

Working out:

• Equation of all the points lying on Circle C:   
• Equation of all the points lying on Circle R: 
• Equating both the equations, will give us the equation of the line that passes these intersection points:

Thus, the line segment that passes through the intersection points of Circle C
and R should have itsequation as

Answer: D

Given

• Circle with diameter AB
  • Length of the diameter = AB = 4 units
• Right triangle ACB
  • ∠CAB = 30
• Hypotenuse AB = 4 units

To Find : y – coordinate of point C

Approach:

• Since AB coincides with the x-axis, the y-coordinate of point C will be equal to the perpendicular distance of point C from AB

So, referring to the above figure, we can write: y – coordinate of point C = CP
So, in order to answer the question, we need to know the value of CP

• Now, area of right triangle ACB = ½ * AB * CP
  • We already know the measure of AB. So, if we find the area of the triangle, we’ll be able to find CP
• We can write another expression for the area of right triangle ACB:
  • Area of right triangle ACB = ½ * AC * BC
• In right triangle ACB, we know the measure of side AB and angle CAB = 30 and angle ACB = 90^o
  • Thus, angle ABC = 180^o – 30^o – 90^o = 60^o
  • WE can conclude that triangle ABC is a 30-60-90 Triangle.
  • So, using the side ratio property of 30-60-90 Triangle, we can easily find AC and BC, and hence the area of the triangle.

Working out:

Finding BC and AC
In right triangle ACB,

• BC : AC : AB = 1 : √3 : 2
  • BC : AB = 1 : 2
  • Since AB = 4
  • So, BC = 2 units
• AC : AB = √3 : 2
  • Since AB = 4
  • So, AC = 2√3units

1. Finding the area of triangle ACB
Area of right triangle ACB = ½ AC * BC = ½ * 2√3 * 2 =
2√3 square units

2. Finding CP
½ * CP * AB = 2√3 square units
½ *CP * 4 = 2√3
CP = √3 units

3. Getting to the answer
Therefore, the y-coordinate of point C =CP = √3 units
Looking at the answer choices, we see that the correct answer is OPTION D

Step 1 & 2: Understand Question and Draw Inference

Given: Parallelogram ABCD has all its sides equal
To find: If ABCD is a square?
So, we need to find if one of the angles of ABCD is a right angle.

Step 3 : Analyze Statement 1 independent

(1) Statement 1 states that "The lines connecting AC and BD have the product of their slopes equal to -1"

• The diagonals are perpendicular to each other. Hence ABCD may be a rhombus or a square.
  • Thus, Statement 1 is Insufficient to answer the question.

Step 4 : Analyze Statement 2 independent

•  (2) Statement 2 states that "Points A and D have the same x-coordinates"
  • ∠DAB would be equal to 90 if points D and A have the same x-coordinates and A and B have the same y-coordinates.
  • The statement does not tell us about the y-coordinates of A and B.
    • Thus, Statement 2 is also Insufficient to answer the question.

Step 5: Analyze Both Statements Together (if needed)

•  Combining the statements does not give us any extra information about the parallelogram ABCD.
• Hence both statements together are also insufficient to answer the question.

Thus, the correct answer is Option E .

Given

3 lines:

• y – x = 2
• 3x + 4y = 29
• y = 2

To Find : The area of the triangle formed between these 3 lines

Approach:

• In order to find the area, we first need to know the coordinates of the 3 vertices of the triangle formed.
• Each vertex of the triangle is the point of intersection of 2 of these 3 given lines. So, we’ll solve each pair of 2 lines to determine their point of intersection (that is, the vertices of the triangle)
• Then, we’ll plot these plots in the x-y plane and find the area of the triangle.

Working out:

Finding the vertices of the triangle

• Let’s find these vertices one by one:
• Intersection of y-x =2 and 3x +4y =29
  • From y – x = 2, we get y = x + 2
  • Substituting this in the equation 3x + 4y = 29, we get:
  • 3x + 4(x+2) = 29
  • 7x + 8 = 29
  • 7x = 21
  • So, x = 3
  • And, y = 3+2 = 5
  • So, one vertex of the triangle is (3,5)
• Intersection of y-x =2 and y=2
  • Putting y = 2 in y – x = 2, we get 2 – x = 2. So, x = 0
  • So, the 2 vertex of the triangle is (0,2)
• Intersection of 3x +4y =29 and y=2
  • ​Putting y = 2 in 3x + 4y = 29, we get 3x + 4(2) = 29
  • 3x = 21
  • So, x = 7
  • The y-coordinate of this vertex will of course be 2 only
  • So, the 3 vertex of the triangle is (7,2)
• So, we can represent the triangle as under:

Finding the area of the triangle

Looking at the answer choices, we see that the correct answer is Option D

Given

• Region R is bounded by
  • 2x + |4y| = 20 and
  • x=0, whereas
• Region P is bounded by
  • |4x| + 2y = 20 and
  • y = 0
• A(B) = area of Region B

To Find: |A(P) – 2A(R)|?

• We need to find the area of regions P and R to answer the question

Approach

• Region R
  • For finding the area of region R, we need to draw the following line segments:
    • x = 0
    • 2x +4|y| = 20. As we are given |y|, the value of |y| will depend on the value of y
      • If y ≥0, then |y| = y.
        • So, we have equation of the line segment as 2x + 4y = 20, i.e. x + 2y = 10 and
      • If y < 0, then |y| = -y.
        • So, we have equation of the line segment as 2x – 4y = 20, i.e. x – 2y = 10
  • Once we draw these line segments, we will find the area of the region bounded by the line segments using standard formulas.
• Region P
  • For finding the area of region R, we need to draw the following line segments:
    • y = 0
    • |4x| + 2y = 20. As we are given |x|, the value of |x| will depend on the value of x.
      • If x ≥0, then |x| = x.
        • So, we have the equation as 4x + 2y = 20, i.e. 2x + y = 10 and
      • If x < 0, then |x| = -x.
        • So, we have the equation of the line segment as 4x – 2y = -20, i.e. 2x – y = -10
• Once we draw these line segments, we will find the area of the region bounded by the line segments using standard formulas

Working out

1. Finding A(R)
a. Assuming y-axis to be the base, we have EF = 5 – (-5) = 10
b. Height = x-coordinate of point D = 10
c. Area of region R = ½ * 10 * 10 = 50
d. A(R) = 50……. (1)

2. Finding A(P)
a. Assuming x-axis to be the base, we have BD = 5 – (-5) = 10
b. Height = y-coordinate of point A = 10

c. Area of region P = ½ * 10 * 10 = 50
d. A(P) = 50…….(2)

3. Using (1) and (2), we have
a. |A(P) – 2A(R)| = | 50 – 2*50| = |-50| = 50
Answer: C

Step 1 & 2: Understand Question and Draw Inference

• Circle C with center at (0, 0)
• Line l intersects the circle at A and B
• OD is perpendicular to AB, where D is a point on line segment AB with coordinates (1, -1)
  • As OD is a perpendicular from the center of circle C to chord AB, D must be the midpoint of AB

• Since the coordinates of point O are (0,0) and of point D are (1, -1), Slope of line OD =  
  • Slope of line AB * Slope of line OD = -1
  • (Slope of line AB)*(-1)= -1
  • Slope of line AB = 1
• Since we’ve inferred that the slope of line AB is 1, we can write the Equation of line AB as: y = 1*x + c, that is, y = x + c
  • As AB passes through (1, -1), we have -1 = 1 + c, i.e. c = -2
  • Equation of line AB : y = x – 2
• To find: Radius of the circle, say r, That is, the length of OA (or OB)
  • To answer this question, we need the coordinates of points A or B so that we can then find the distance between points O(0,0) and points A or B.

Step 3 : Analyze Statement 1 independent

(1) The x intercept of line l is 2.
We know from the equation of the line, that x- intercept of the line is 2. Hence, there is no added information provided.

Insufficient to answer

Step 4 : Analyze Statement 2 independent

(2) The product of the x coordinates of points A and B as well as the product of the y coordinates of points A and B is zero.

• Let the coordinates of point A be (x₁, y₁) and coordinates of point B be(x₂ , y₂).
• x * x = 0
  • Either of x or x or both are zero
• y * y = 0
  • Either of y or y or both are zero
• x and y both cannot be zero, as that would mean that point A is the origin. Similarly x and y cannot be zero at the same time.
• So, coordinates of point A and B can be (0, y ) and (x , 0) or vice versa, i.e. they lie on the y-axis and the x-axis respectively.
• Now, we know that equation of line AB : y = x – 2.
  • Putting coordinates of point A(0, y ) in the equation, we have y = 0 – 2, i.e. y = -2
  • So, Coordinates of point A(0, -2)

As we know the coordinate of point A, we can calculate the radius of the circle C.
Sufficient to answer.

Step 5: Analyze Both Statements Together (if needed)

As we have a unique answer from step-4, this step is not required.
Answer: B

Step 1 & 2: Understand Question and Draw Inference

To Find:

• Is the slope of line l negative?

Step 3 : Analyze Statement 1 independent

(1) Statement 1 states that "The line passes through quadrants II and III".

• Following cases are possible:
  • If the line also passes through quadrant-I, the slope of the line will be positive
  • If the line also passes through quadrant- IV, the slope of the line will be negative.
  •  If the line passes through quadrants II and III only and is parallel to y-axis, the slope of the line will be infinity.

Hence, Statement 1 is insufficient to answer

Step 4 : Analyze Statement 2 independent

(2) Statement 2 states that "For each pair of coordinates (x, y) lying on the line l, the product of x and y is not always non-negative."

• x * y < 0 for some points on line l. This is possible when the line passes through either quadrant-II, IV or both:
  • If Line l passes through quadrant- II but not quadrant-IV, then Slope of the line is positive
  • If Line l passes through quadrant- IV but not quadrant-II, then Slope of the line is positive
  • If Line l passes through both quadrant –II and IV, then Slope of the line is negative

Hence, Statement 2 is insufficient to answer

Step 5: Analyze Both Statements Together (if needed)

1. Line l passes through quadrants-II and III
2. Line l passes through quadrant II, or IV or both

Following cases are possible:

• Line l passes through quadrants II, III and IV : Slope of the line is negative
• Line l passes through I, II and III : Slope of the line is positive

As we do not have a unique answer, hence by combining both the statements also it is insufficient to answer the question.
Thus, the correct answer is Option E .

Given

• The given information corresponds to the following diagram:

To Find: Area of quadrilateral ABCD

Approach

1. To find the area of quadrilateral ABCD, we’ll use the method of addition and subtraction of areas.

• We will extend the quadrilateral such that it forms rectangular figures – rectangles or right-angled triangles. This can be done as under:

2. So, Area of Quadrilateral ABCD = (Area of Rectangle QBPS) – (ar ΔAPB + ar ΔBQC + ar ΔCRD + ar of square DRST + ar ΔATD)

Looking at the answer choices, we see that the correct answer is Option D