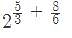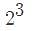Test: Exponents- 1 - GMAT MCQ
15 Questions MCQ Test Quantitative for GMAT - Test: Exponents- 1
If n is a positive integer greater than 2, what is the greatest prime factor of 3n + 3n + 3n – 3n-2?
If ‘x’ and ‘y’ are non-negative integers, what is the value of x + y?
(1) x4 is even, where x is a prime number.
(2) xy is odd.
Find the value of n that satisfies the equation 2(-3)4n = 18(27)n+2
The intensity of radiation emanating from a nuclear event is measured on an exponential scale where the second and fourth points indicate intensities of 25 and 625, respectively. On that scale, what would the intensity at the third point be?
Positive integer P lies between 1 and 30. What is the value of P?
(1) P has at least two prime factors
(2) The cube of P is less than 300
The half-life of a radioactive element is defined as the amount of time required for the amount of the element to decrease by half. If the half-life of an element is 3 years, how long will it take for the element to be reduced to one-eighth of its original amount?
Is xy ≥ 1 if both x and y are non-zero integers?
(1) y = -x
(2) y = 2k where k is a non-zero integer
Find the value of positive integer P that lies between 1 and 30 and is a perfect square.
(1) P has at least one Prime factor
(2) The cube of P is less than 300
If k is an integer then find the value of
(1) 2r – 2k = 26, where r is an integer
(2) 14 + k = 3k – 2r, where r is an integer
|
115 videos|106 docs|113 tests
|



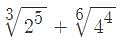
 +
+ 
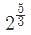 +
+ 
 +
+