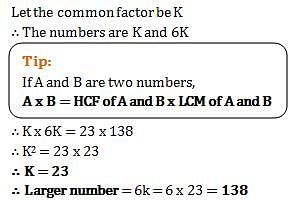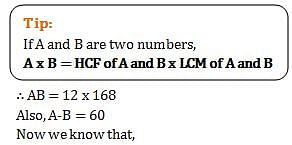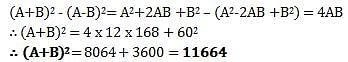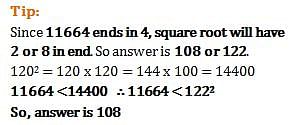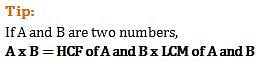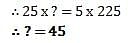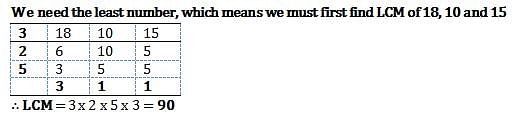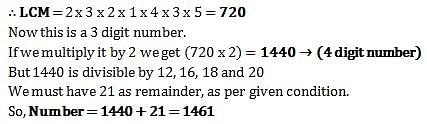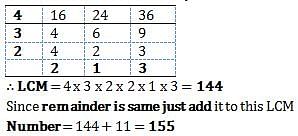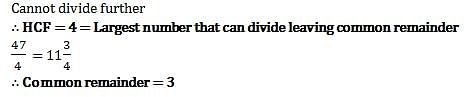Test: LCM & GCD - 2 - GMAT MCQ
20 Questions MCQ Test Quantitative for GMAT - Test: LCM & GCD - 2
If the product of two positive integers is 144, which of the following could be the LCM and HCF of the two numbers?
I. LCM : 24; HCF : 6
II. LCM : 18; HCF : 8
III. LCM : 16; HCF : 9
I. LCM : 24; HCF : 6
II. LCM : 18; HCF : 8
III. LCM : 16; HCF : 9
LCM of two numbers is 138. But their GCD is 23. The numbers are in a ratio 1:6. Which is the largest number amongst the two?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The least common multiple of two numbers is 168 and highest common factor of them is 12. If the difference between the numbers is 60, what is the sum of the numbers?
If least common multiple of two numbers is 225 and the highest common factor is 5 then find the numbers when one of the numbers is 25?
The greatest number of four digits which is divisible by 15, 25, 40, 75 is
What is the least number which when divided by the numbers 3, 5, 6, 8, 10 and 12 leaves in each case a remainder 2 but which when divided by 13 leaves no remainder?
When a number is divided by 893 the remainder is 193. What will be the remainder when it is divided by 47?
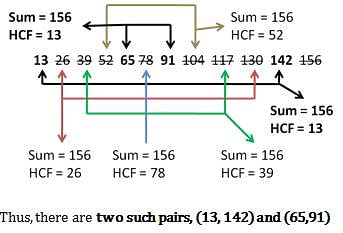
The sum of two numbers is 156 and their HCF is 13. The numbers of such number pairs is
The L.C.M. of two numbers is 14560 and their H.C.F. is 13. If one of them is 416, the other is
The greatest length of the scale that can measure exactly 30 cm, 90 cm, 1 m 20 cm and 1 m 35 cm lengths is
What will be least number of marbles with Rohit if he can arrange them in rows of 18, 10 and 15 marbles each as well as make a perfect solid square out of all the marbles?
3 birds fly along the circumference of a jungle. They complete one round in 27 minutes, 45 minutes and 63 minutes respectively. Since they start together, when will they meet again at the starting position?
What least possible 4-digit number, when divided by 12, 16, 18 and 20 leaves 21 as remainder?
5 clocks ring automatically at intervals of 12 minutes, 8 minutes, 3 minutes, 4 minutes and 10 minutes, respectively. In 8 hours from the moment they start, how many times will they ring together?
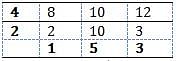
What least number when divided by 36, 24 and 16 leaves 11 as remainder in each case?
If (x - 4) is the HCF of x2 - 8x + 15 and x2 - kx +1 , then what is k?
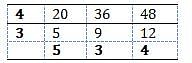
What least number when divided by 20, 48 and 36 leaves the remainders 13, 41 and 29, respectively?
There are 3 equilateral triangles with sides 114cm, 76cm and 152 cm. What maximum size scale can measure them exactly?
What greatest number divides 17, 42 and 93 and leaves remainders 4, 3 and 15, respectively?
What largest number will divide 47, 35 and 27 leaving same remainder in each case? What will be the common remainder?
|
115 videos|106 docs|113 tests
|
|
115 videos|106 docs|113 tests
|