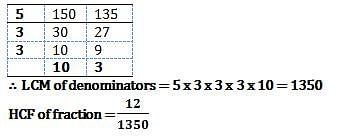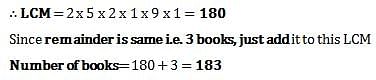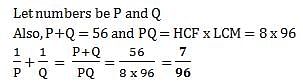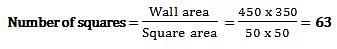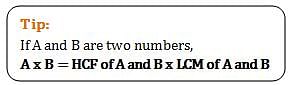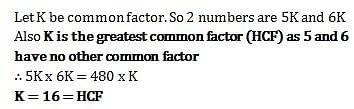Test: LCM & GCD - 3 - GMAT MCQ
15 Questions MCQ Test Quantitative for GMAT - Test: LCM & GCD - 3
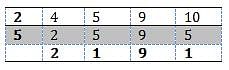
Rajesh had to arrange his books in uniform groups. He makes groups of 4 books each. But 3 books are left. He tries it with groups of 5 books each. But still 3 books are left. 3 books are still left when he tried with groups of 9 or 10 books each. How many books does he have?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
HCF and LCM of two numbers is 8 and 96. Sum of those numbers is 56. Then what is sum of their reciprocals?
Manoj wants to paste wallpaper on wall of his room. The wall is 4 meters and 50 cm in length and 3 meters and 50 cm in height. But the wall should be covered completely only by square pieces of wallpaper having same size. What is the number of maximum sized wallpaper squares needed to cover the walls completely?
The ratio of two numbers is 5 : 6 and their LCM is 480, then their HCF is?
The length and breadth of a rectangular floor are 16.25 metre and 12.75 metre respectively. Find how many minimum number of square tiles would be required to cover it completely?
The L.C.M. of two number is 60. The numbers are in the ratio 4 : 5. Find the sum of numbers.
Find the least number which should be added to 2430 so that the sum is exactly divisible by 5, 4 and 2
The ratio of two numbers is 4 : 5 and their H.C.F is 4. Find their L.C.M.
A man decides to pave with square tiles his hall which is 4.8 metres long and 5.38 metres wide. Find the largest size of the tile that he could use.
3 bells beep at an interval of 12, 20, and 35 minutes. If they beep together at 10 a.m., then they will again beep together at:
The least number which is a multiple of 11 and when divided by 3, 5 and 9 leaves 2 as remainder:
LCM of two numbers is 495. HCF of these numbers is 5. If the sum of the numbers is 100, find out the difference between the two numbers.
|
115 videos|106 docs|113 tests
|
|
115 videos|106 docs|113 tests
|