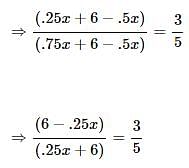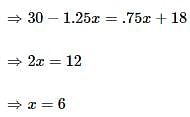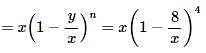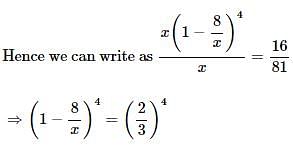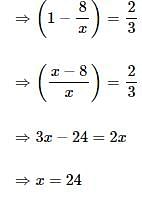Test: Mixtures- 1 - GMAT MCQ
15 Questions MCQ Test Quantitative for GMAT - Test: Mixtures- 1
What is the ratio of milk to water in a milk solution, if the solution contains only these 2 ingredients?
I) The volume of milk is 80% of the total solution.
II) The volume of water is 20% of the total solution.
50 ml of water is added to 50 ml of alcohol solution which is 50% alcohol. What is the final concentration of this alcohol mixture?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A 30% alcohol solution (only alcohol & water) is poured into a container having a 60% alcohol solution (only alcohol & water). If the resultant mixture has 50% alcohol, then what is the ratio in which the 30% solution is mixed with the 60% Alcohol solution?
A solution X is 80% A and 20% B. Another solution Y is 60% B and 40% C. If 6 litres of Solution X is mixed with 2 litres of Solution Y, then what is the concentration of compound B in the final solution?
A juicy fruit X contains 70% water and remaining is pulp. If the fruit X is dried to remove the entire water and now weighs 180 grams, what was the original weight of the fruit?
How many liters of a 60% alcohol solution must be added to 50 liters of a 40% alcohol solution to result in 50% alcohol solution?
How much water should be added (in liters) to 2 liters of milk having 3% fat to reduce the concentration of fat to 1% by volume?
A Lentil mixture is prepared using 2 different types of lentils: yellow and red. The ratio, in grams, of yellow lentils to red lentils is 3:2. How many grams of yellow lentils are in the mixture?
(1) The ratio of the densities (mass per unit volume) of yellow lentil to red lentil is 2:3.
(2) If 50 grams of yellow lentils are removed from the mixture, the ratio of yellow to red in the resulting mixture is 5:4
A solution of salt and water has a volume of 1 Gallon. The solution is heated on the flame and consequently the volume of the solution decreased because some water evaporated. What is the percentage of salt by volume in the resultant solution?
(1) The initial solution contained 10% salt by volume.
(2) The volume of the final solution is 3/4 Gallon.
A smoothie with 2% strawberry syrup and 5% mango syrup is made in milk. How much more strawberry syrup (in litres) must be added to 12 litres of smoothie so that the smoothie contains 4% strawberry syrup by volume?
Juice A contains 60% orange juice, 20% apple juice and 20% carrot juice. Juice B contains 20% orange juice and 80% carrot juice. If a juice concoction is made such that it contains 50% carrot juice, how much juice A is added as a percentage of the juice concoction?
A box initially contains 300 balls of which 40% are red and the rest are green. 50% more red balls are then added to the box. By what percent should the number of red balls be increased further to decrease the percent of green balls to 40%?
In what ratio did a grocer mix three varieties of tea that cost $6 per kg, $7 per kg and $8 per kg respectively, to make a profit of 10% by selling the mixture at $7.70 per kg?
(1) The grocer mixed 135 kg of the variety of tea that costs $7 per kg.
(2) The weight of the mixture was 315 kg.
A milk vendor has 2 cans of milk. The first contains 25% water and the rest milk. The second contains 50% water. How much milk should he mix from each of the containers so as to get 12 litres of milk such that the ratio of water to milk is 3 : 5?
8 litres are drawn from a cask full of wine and is then filled with water. This operation is performed three more times. The ratio of the quantity of wine now left in cask to that of the water is 16 : 65. How much wine did the cask originally hold?
|
115 videos|106 docs|116 tests
|
|
115 videos|106 docs|116 tests
|