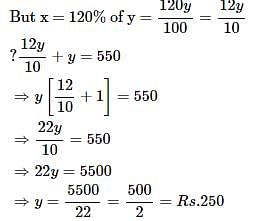Test: Percentages- 2 - GMAT MCQ
20 Questions MCQ Test Quantitative for GMAT - Test: Percentages- 2
A toy manufacturer runs his plant for 30 days in a month such that his daily output is constant during the month. He undertakes the maintenance of his plant every 6 months for 5 days in a month, during which period no toys are produced. As he has to undertake the maintenance of the plant this month, he increases his constant daily output of toys by 10 percent compared to the last month’s constant daily output. If the manufacturer wants to keep his monthly revenue unchanged as compared to last month, by approximately what percentage should be increase the price per toy?
If b is a prime number, what percent of 3 is b?
(1) b is more than 200% greater than 2 and less than 40% of 32
(2) 3b/7 is 40% less than 5
(1) b is more than 200% greater than 2 and less than 40% of 32
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The population of city X increased by 10% in year 2013 and 15% in year 2014. What is the approximate population of the city at the
end of year 2014, if population of the city at the starting of year 2013 was 21,000?
end of year 2014, if population of the city at the starting of year 2013 was 21,000?
The price to earnings ratio of the pharmaceutical industry on a stock exchange was p at the beginning of the year 2014 and q at the end of the year 2014. Company X, which was a pharmaceutical company had its earnings to price ratio equal to a at the beginning of the year 2014 and b at the end of the year 2014. By what percentage was the percentage increase in the price to earnings ratio of company X less than that of the pharmaceutical industry?
An airline allowed free baggage only up to 20 kilograms of weight. Each extra kilogram of weight cost a passenger $5 per kilogram. Of the total weight of the baggage that Roger was carrying, 60 percent of the weight was more than the free baggage allowance. If the total ticket cost of Roger including the excess baggage fare was $600, by what percentage did his ticket cost increase because of the excess baggage that he was carrying?
An internet-based company that came into business on January 1, 2015 acquired 250 customers in the first month. If the company
had 20% month-on-month growth for the next 2 months and 10% month-on-month growth after that, how many customers did the
company have on May 1, 2015?
If x and y are positive numbers, x is what percent of y?
(1) 3x is 72% of 2y
(2) y = 2x + 1
An army’s recruitment process included n rounds of selection tasks. For the first a rounds, the rejection percentage was 60 percent per round. For the next b rounds, the rejection percentage was 50 percent per round and for the remaining rounds, the selection percentage was 70 percent per round. If there were 100000 people who applied for the army and 1400 were finally selected, what was the value of n?
A company had 1000 employees at the beginning of the year 2011. If p percent of the employees present at the beginning of the year left the company during the year and the number of employees at the end of the year was r percent greater than the number of employees at the beginning of the year, how many employees joined the company during the year 2011?
(1) p + r = 30
(2) Had the number of employees leaving the company been r percent of the employees at the beginning of the year and the number of employees at the end of the year been p percent greater than the number of employees at the beginning of the year, the number of employees who joined the company would have remained the same.
The price of a consumer good increased by p% during 2012 and decreased by 12% during 2013. If no other change took place in
the price of the good and the price of the good at the end of 2013 was 10% higher than the price at the beginning of 2012, what was
the value of p?
A soccer team played 25% more matches year-on-year in the second year of its formation. It won 84% of the matches it played in the second year, which was an improvement of 5% over the percentage of matches won in the first year. In the third year, the team played 4% fewer matches year-on-year but lost only 12.5% of the matches it played, which was one less than the number of matches lost by the team in the second year. Which of the following statements must be correct?
- The team lost the same number of matches in the first yea and the second year
- The team won the same number of matches in the second year and the third year
- The team played five more matches in the third year than the first year
Daniel was going to purchase an electronic item from a brickand- mortar retail store that offered a discount of 10% on the marked price of the item. Sometime before the purchase, however, he discovered that the same item was also available on an ecommerce website. Though the customers of the ecommerce website had to bear overhead costs of 10% over the marked price, including taxes and delivery charges, the marked price of the item at the retail store was 25% higher than the website. If Daniel wanted to minimize his expense on the item, through which of the two channels – brick-and-mortar retail store and ecommerce website – should he have bought the item and what would have been his percent savings with respect to the other channel?
In a class of 100 students, the percentage of boys in the class is equal to the percentage of students who pass in a test. If 2 out of
every 3 girls in the class pass the test and the number of boys who do not pass the test is 10 less than the total number of girls in the
class, which of the following is the closest to the percentage of boys who passed the test?
The temperature of a place at noon on a certain day is 25% higher than the temperature of the same place at midnight on the same
day. What the temperature of the place at midnight?
(1) The temperature of the place at midnight is 20% lower than the temperature of the same place at noon
(2) The temperature of the place at noon is 10 units greater than the temperature of the place at midnight
A wedding decorator receives two sets of light bulbs- A and B. Set A consists of 100 light bulbs of which 20 percent are defective and set B consists of 80 light bulbs of which 50 percent are defective. If the light bulbs from the two sets are mixed, what is the minimum percentage of light bulbs the decorator needs to take out to make sure that the remaining light bulbs are non-defective?
Abe and Beth both start from a common point and travel in different directions towards their respective destinations. Abe’s
average speed is 25% greater than Beth’s average speed but Abe needs to cover 50% greater distance than Beth. Which of the
following is closest to the percentage by which the travel time of Beth lesser than that of Abe?
Five friends Adi, Brian, Close, Derek and Eli appeared in two aptitude tests. In the first aptitude test, Derek’s score was 50 percent less than the average (arithmetic mean) score of the five people. In the second aptitude test, Derek scored 50 percent more than what he scored on the first aptitude test. If the scores of his friends in the second aptitude test were same as their scores in the first aptitude test, by approximately what percentage was Derek’s score less than the average (arithmetic mean) score of the 5 people in the second aptitude test?
if A = x% of y and B = y% of x, then which of the following is true?
Two employees X and Y are paid a total of Rs. 550 per week by their employer. If X is paid 120 percent of the sum paid to Y, how much is Y paid per week?
In a competitive examination in State A, 6% candidates got selected from the total appeared candidates. State B had an equal number of candidates appeared and 7% candidates got selected with 80 more candidates got selected than A. What was the number of candidates appeared from each State?
|
110 videos|110 docs|120 tests
|
|
110 videos|110 docs|120 tests
|