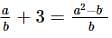Test: Simplifying Expression - GMAT MCQ
15 Questions MCQ Test Quantitative for GMAT - Test: Simplifying Expression
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
What is the highest integral value of 'k' for which the quadratic equation x2 - 6x + k = 0 will have two real and distinct roots?
If a and b are integers such that a > b > 0, what is the minimum value of (a2 + b2) (a+b) (a-b) + 2b4?
What is the value of where a ≠0?
(i) a = 8
(ii) b = 16a
If (a + b)2 = x and (a – b)2 = y, then what is the value of 2ab in terms of x and y?
If x, y, z are non-zero numbers and x + xy2 = z3, then which of the following is NOT equal to 1?
What is the sum of the squares of x2 and y2?
(1) x8 – y8 = 6
(2) x4 – y4 = 2
For how many real values of x is this expression equal to zero?
, where x ≠ -1 and x ≠ 1
If x is replaced with - 1/x in the expression P, the expression Q is obtained. Which of the following is the correct relationship between P and Q?
If y >2, and which of the following could be the value of 2x + 3?
|
110 videos|110 docs|120 tests
|
|
110 videos|110 docs|120 tests
|


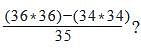
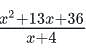 where x =1/4
where x =1/4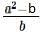 }, then 2b =
}, then 2b =