Test: Statistics- 1 - GMAT MCQ
15 Questions MCQ Test Quantitative for GMAT - Test: Statistics- 1
A set X: {a1, a2, a3, a4, a5} with non-zero elements have mean M. What is the mean of the set Y: {a1 - 1, a2 - 2, a3 - 3, a4 + 5, a5 + 1}?
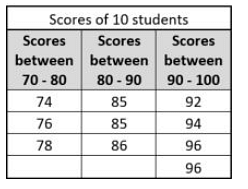
If scores of 10 students in a class are arranged in the table (shown below), then what is the Median of their scores?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
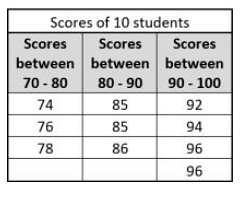
If scores of 10 students in a class are arranged in the table (shown below), then what is the Range of their scores?
Set X is given by {a, 2a, 3a, 4a, 5a} where ‘a’ is a positive integer. If element ‘a’ in Set X is replaced by ‘b’ and b < a, then which of the following must be true?
I.Mean would not change.
II.Median would not change.
III. Standard deviation would not change
Set A: {-11, 0, 0, 11}
Set B: {2, 4, 6, 8}
Set C: {50, 51, 52, 53}
Set D: {12, 12, 12, 12}
Which of the following sets have a maximum & minimum standard deviation respectively?
If the medians of the List A and List B are same, what is the value of k?
List A: 2, 5, 7, 20
List B: 2, 5, 7, 20, k
What is x, if the average of five numbers, x, 6, 3, 15 and 12 is equal to the median?
(1) 6 < x < 12
(2) x is median of the five numbers
A, B, C, D, E, and F are six consecutive positive odd integers in increasing order. What is the value of the median of these six integers?
(1) The sum of the two smallest integers is greater than the largest integer by 13
(2) The average (arithmetic mean) of these integers is 26
10, 6, p, q, 11
Given the above series of positive integers arranged in a random order, what is the value of p/q?
(1) The average (arithmetic mean) of given numbers is 7
(2) p is the median of the given series
From January to October, the revenue of a textile manufacturing plant averaged 20,000 USD per month. What average monthly revenue in USD was required in November and December, if the plant had a goal to achieve 330,000 USD in revenue by the end of the calendar year?
What is the mean of an increasing sequence of 10 consecutive integers?
(1) The mean of the first 7 integers is 7.
(2) The mean of the last 7 integers is 10.
What is the standard deviation of {-3, -6, -5, -10} approximately equal to, if the standard deviation of {3, 6, 5, 10} is approximately equal to 2.5?
Some milk was added to each of the 5 cans. If standard deviation of the quantity of milk in the 5 cans at the beginning was 3.5 liters, what was the standard deviation of the quantity of milk in the 5 cans at the end?
(1) In each can, 20% of existing amount of milk was added.
(2) The average volume of milk in the cans at the end was 25 liters.
Set X consists of 10 integers and has median of 20 and a range of 20. What is the value of the greatest possible integer that can be present in the set?
S is standard deviation of a, b, and c, if a constant C is added to all the three digits, the new standard deviation will be?
|
115 videos|106 docs|113 tests
|
|
115 videos|106 docs|113 tests
|

















