Test: Time And Work- 2 - GMAT MCQ
20 Questions MCQ Test Quantitative for GMAT - Test: Time And Work- 2
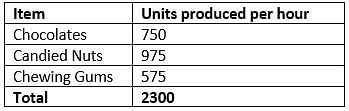
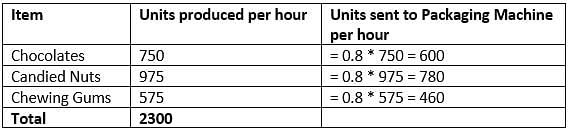
At a food processing and packaging plant, identical packets of confectionary items are prepared at a constant rate by a packaging machine. Each packet contains 3 chocolates, 4 candied nuts and 2 chewing gums. The production rate of chocolates, candied nuts and chewing gums at the plant is 750, 975 and 575 units per hour respectively. All the produced items are immediately sent to a common quality checking machine that can process 3000 units of confectionary items per hour. 20 percent each of chocolates, candied nuts and chewing gums fail the quality check. The remaining items are sent to the packaging plant without any holdup or delay. Which of the following can represent the number of packets of confectionary items prepared by the packaging machine in one hour?
I. 195
II. 230
III. 280
II. 230
III. 280
Operating at their respective constant rates, Photocopying machine B takes 6 minutes more than photocopying machine A to copy x pages. When machines A and B are operated simultaneously, 7x pages can be copied in 20 minutes. In how many minutes can machine A operating alone copy 2x pages?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Peter, Mark and John work in the marketing department of an e-learning firm. Peter can answer 25 emails in an hour, Mark can answer 40 percent more emails in an hour than Peter and John takes 1/6 lesser time to answer the same number of emails as Peter. By what percentage should Peter increase his speed so that the three employees can together answer 1/6 more emails than they currently do?
If John produces n units of an item in t hours, what is the value of n?
(1) If John produces 4 more items per hour, he would take 1/4 lesser time to produce n units of the item.
(2) If John increases his rate of production by 25 percent, the time taken by him to produce n items would be 80 percent of the original time.
Transmitting data at the same constant rate, 12 identical cables can transmit x bits of digital information per minute. How many bits of information can be transmitted by 27 such cables in 25 seconds?
The water from outlet A, flowing at a constant rate, can fill a rectangular swimming pool in 12 hours while the water from outlet B, flowing at a constant rate, can fill the same swimming pool in 18 hours. On a day when the pool was empty, outlet A was opened at 7 AM and outlet B was opened at 10 AM. Outlet A was closed at 2 PM and outlet B was closed at 4 PM. If there was no water flow from outlet A between 10:30 AM to 11:30 AM because of maintenance work, the height of the water in the pool at 4 PM was approximately what percentage of the depth of the pool?
If 30 machines, each working at the same constant rate, together can produce n/2 units of an item in 15 days, how many machines will be needed to produce 2n units of the item in 45 days?
A rectangular tank has the dimensions of its base as 30 metres by 20 metres and a height of 10 metres. There are two taps attached to the tank such that each tap working alone at a constant rate can fill the tank completely in 60 hours and 90 hours respectively. One of the walls of the tank has holes along the height of the tank at a regular distance of 2 metres and the first such hole is 2 metres above the base of the tank. The rate of water outflow from each hole is 10m per hour. If both the taps are opened simultaneously in the empty tank, approximately how many hours will it take to fill the tank completely?
4 identical machines, which operate at the same constant rate, together started manufacturing the batch of an item at 2 PM. Did
they finish the batch before 3.30 PM?
(1) The batch size was between 200 and 210 units, inclusive, of the item
(2) One machine could manufacture between 30 and 50 units, inclusive, of the item in 1 hour
A container is completely filled with a sugar solution composed of water and sugar syrup in the ratio of 7:3. The container has 2 holes covered with filters such that from one of the holes only sugar syrup can flow out and from the other hole only water can flow out. The rates of water outflow and sugar syrup outflow from their respective holes are x cubic centimeters per hour and y cubic centimeters per half an hour respectively, such that x:y = 5:1. If the water from the solution can be drained out completely in 14 hours from the hole, how much time in hours would it take the container to be empty if both the holes are opened simultaneously?
An automated manufacturing plant uses robots to manufacture products. A generation-I robot working alone can manufacture a product in 30 hours whereas a generation-II robot working alone can manufacture the same product in 20 hours. If the manager of the plant wants the product manufacturing time to be greater than equal to 5 hours with at least 1 robot each of both generations working together, how many possible combinations of the number of robots of each generation is possible?
Two machines A and B worked at variable rates. The average number of items produced per day by machine A could be expressed as Ra (x) = ax(x + 1) and the average number of items produced per day by machine B could be expressed as Rb (x) = bx(x-1), where x was the number of consecutive days worked and a, b were constants. If machine B produced 90 more items when it worked for 4 consecutive days than when it worked for to 3 consecutive days and machine A produced a total of 232 items when it worked in two intervals of 3 consecutive days and 4 consecutive days, how many items was produced by machines A and B working together for 10 consecutive days?
John starts reading a book from the first page onwards and reads each page only once. Every day, he reads twice the number of pages read by him the previous day. If the book has 400 pages, will John still be reading the book on the 6 day after he starts reading it?
(1) On the fifth day of reading the book, John reads more than 180 pages
(2) John reads 52 more pages on the fourth day of reading the book than he reads on the third day
Two machines A and B work at constant rates which are in the ratio of 1:2 respectively. If the two machines work together, they can complete 1/3rd of a job in 3 hours. If machine A starts working on the job and works alone for 18 hours, how many hours would machine B working alone take to complete the remaining work?
Machines M and N produce identical widgets but at different constant rates. Machine M takes 10 hours to produce 1000 widgets and Machines M and N together take 6 hours and 40 minutes to produce 2000 widgets. How much time does Machine N take to produce 3000 widgets?
A rectangular reservoir is filled with water till one-fifth of the height of the reservoir. If an outlet at the bottom of the reservoir is unplugged, the water in the reservoir will drain completely in 1 hour. If the outlet remains plugged and the inlet tap at the head of the reservoir is opened, the reservoir will fill to the brim in 2 hours. In how much time will the reservoir fill to the brim if the outlet is unplugged 30 minutes after the inlet tap is opened?
On the first day of the launch of an anticipated electronic item, a queue formed outside an exclusive electronics store that sold the item. At the time the store opened, the queue had 60 people in it and throughout the day, a new person joined the queue every 3 minutes. That day, the store served, only the people in the queue, at a constant service rate of 30 people per hour. If no person re-joined the queue upon getting served once, how many people were in the queue 4 hours after the store opened?
A is thrice as good as B in work. A is able to finish a job in 60 days less than B. They can finish the work in - days if they work together.A.
A can do a particular work in 6 days . B can do the same work in 8 days. A and B signed to do it for Rs. 3200. They completed the work in 3 days with the help of C. How much is to be paid to C?A.
6 men and 8 women can complete a work in 10 days. 26 men and 48 women can finish the same work in 2 days. 15 men and 20 women can do the same work in - days.
|
108 videos|103 docs|114 tests
|
|
108 videos|103 docs|114 tests
|