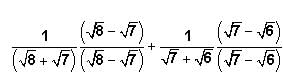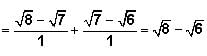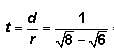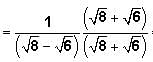Test: Work & Rate - GMAT MCQ
8 Questions MCQ Test Quantitative for GMAT - Test: Work & Rate
Machine A and Machine B can produce 1 widget in 3 hours working together at their respective constant
rates. If Machine A's speed were doubled, the two machines could produce 1 widget in 2 hours working
together at their respective rates. How many hours does it currently take Machine A to produce 1 widget on
its own?
rates. If Machine A's speed were doubled, the two machines could produce 1 widget in 2 hours working
together at their respective rates. How many hours does it currently take Machine A to produce 1 widget on
its own?
Adam and Brianna plan to install a new tile floor in a classroom. Adam works at a constant rate of 50 tiles per
hour, and Brianna works at a constant rate of 55 tiles per hour. If the new floor consists of exactly 1400 tiles,
how long will it take Adam and Brianna working together to complete the classroom floor?
hour, and Brianna works at a constant rate of 55 tiles per hour. If the new floor consists of exactly 1400 tiles,
how long will it take Adam and Brianna working together to complete the classroom floor?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A copy machine, working at a constant rate, makes 35 copies per minute. A second copy machine, working at a constant rate, makes 55 copies per minute. Working together at their respective rates, how many copies do the two machines make in half an hour?
Tom, working alone, can paint a room in 6 hours. Peter and John, working independently, can paint the same room in 3 hours and 2 hours, respectively. Tom starts painting the room and works on his own for one hour. He is then joined by Peter and they work together for an hour. Finally, John joins them and the three of them work together to finish the room, each one working at his respective rate. What fraction of the whole job was done by Peter?
Machine A can complete a certain job in X hours. Machine B can complete the same job in y hours. If A and B work together at their respective rates to complete the job, which of the following represents the fraction of the job that B will not have to complete because of A's help?
Lindsay can paint 1/x of a certain room in 20 minutes. What fraction of the same room can Joseph paint in 20 minutes if the two of them can paint the room in an hour, working together at their respective rates?
One smurf and one elf can build a treehouse together in two hours, but the smurf would need the help of two fairies in order to complete the same job in the same amount of time. If one elf and one fairy worked together, it would take them four hours to build the treehouse. Assuming that work rates for smurfs, elves, and fairies remain constant, how many hours would it take one smurf, one elf, and one fairy, working together, to build the treehouse?
paint crew gets a rush order to paint 80 houses in a new development. They paint the first y houses at arate of x houses per week. Realizing that they'll be late at this rate, they bring in some more painters andpaint the rest of the houses at the rate of 1.25x houses per week. The total time it takes them to paint all thehouses under this scenario is what fraction of the time it would have taken if they had painted all the housesat their original rate of x houses per week?
|
108 videos|103 docs|114 tests
|
|
108 videos|103 docs|114 tests
|


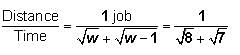
 The COMBINED RATE of machine A and machine B =
The COMBINED RATE of machine A and machine B =