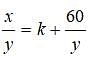Test: Divisibility And Remainders- 2 - GMAT MCQ
15 Questions MCQ Test Quantitative for GMAT - Test: Divisibility And Remainders- 2
When the positive integer x is divided by 9, the remainder is 5. What is the remainder when 3x is divided by 9?
If (x # y) represents the remainder that results when the positive integer x is divided by the positive integer y, what is the sum of all the possible values of y such that (16 # y) = 1?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If k and x are positive integers and x is divisible by 6, which of the following CANNOT be the value of 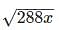 ?
?
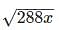 ?
?1025 – 560 is divisible by all of the following EXCEPT:
x, y, a, and b are positive integers. When x is divided by y, the remainder is 6. When a is divided by b, the remainder is 9. Which of the following is NOT a possible value for y + b?
When the integer x is divided by the integer y, the remainder is 60. Which of the following is a possible
value of the quotient x/y?
I. 15.15
II. 18.16
III. 17.17
The ratio of cupcakes to children at a particular birthday party is 104 to 7. Each child at the birthday party eats exactly x cupcakes (where x is a positive integer) and the adults attending the birthday party do not eat anything. If the number of cupcakes that remain uneaten is less than the number of children at the birthday party, what must be true about the number of uneaten cupcakes?
I. It is a multiple of
2. II. It is a multiple of
3. III. It is a multiple of 7.
When the positive integer x is divided by 11, the quotient is y and the remainder 3. When x is divided by 19, the remainder is also 3. What is the remainder when y is divided by 19?
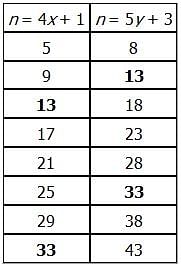
A group of n students can be divided into equal groups of 4 with 1 student left over or equal groups of 5 with 3 students left over. What is the sum of the two smallest possible values of n?
When x is divided by 4, the quotient is y and the remainder is 1. When x is divided by 7, the quotient is z and the remainder is 6. Which of the following is the value of y in terms of z?
If n is an integer and n4 is divisible by 32, which of the following could be the remainder when n is divided by 32?
x1 and x2 are each positive integers. When x1 is divided by 3, the remainder is 1, and when x2 is divided by 12, the remainder is 4. If y = 2x1 + x2, then what must be true about y?
I. y is even II. y is odd III. y is divisible by 3
The sum of all the digits of the positive integer q is equal to the three-digit number x13. If q = 10n – 49, what is the value of n?
If positive integer n is divisible by both 4 and 21, then n must be divisible by which of the following?
Susie can buy apples from two stores: a supermarket that sells apples only in bundles of 4, and a
convenience store that sells single, unbundled apples. If Susie wants to ensure that the total number of
apples she buys is a multiple of 5, what is the minimum number of apples she must buy from the
convenience store?
|
108 videos|103 docs|114 tests
|
|
108 videos|103 docs|114 tests
|


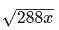 can be simplified to 12√2kx. Given that x is divisible by 6, for the purpose of solving this problem x might be restated as 6y, where y may be any positive integer. The expression
can be simplified to 12√2kx. Given that x is divisible by 6, for the purpose of solving this problem x might be restated as 6y, where y may be any positive integer. The expression 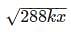 could then be further simplified to
could then be further simplified to 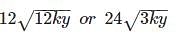
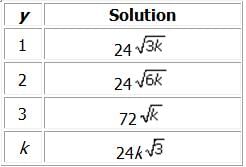
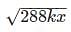 is 24√k. For this expression to be a possible solution, y would have to equal 1/3, which is not a positive integer. Put another way, this solution would require that x = 2, which cannot be true because x is divisible by 6.
is 24√k. For this expression to be a possible solution, y would have to equal 1/3, which is not a positive integer. Put another way, this solution would require that x = 2, which cannot be true because x is divisible by 6.