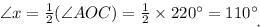Test: Geometry- 1 - Bank Exams MCQ
15 Questions MCQ Test IBPS PO Prelims & Mains Preparation - Test: Geometry- 1
A vertical stick 20 m long casts a shadow 10 m long on the ground. At the same time, a tower casts a shadow 50 m long on the ground. Find the height of the tower.
The area of similar triangles, ABC and DEF are 144cm2 and 81 cm2 respectively. If the longest side of the larger △ABC be 36 cm, then the longest side of the smaller △DEF is:
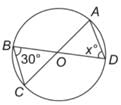
Find the value of x in the figure, if it is given that AC and BD are diameters of the circle.

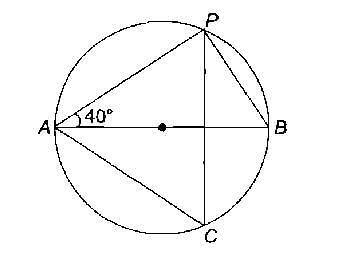
AB is the diameter of the circle and ∠PAB=40∘
what is the value of ∠PCA?
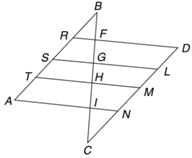
In the figure, AB is parallel to CD and RD || SL || TM || AN, and BR : RS : ST : TA = 3 : 5 : 2 : 7. If it is known that CN = 1.333 BR. Find the ratio of BF : FG : GH : HI : IC
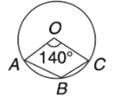
In the following figure, it is given that O is the centre of the circle and ㄥAOC = 140°. Find ㄥABC.
In the figure below, PQ = QS, QR = RS and angle SRQ = 100°. How many degrees is angle QPS?

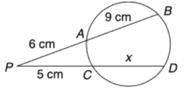
In the given figure, AD is the bisector of ∠BAC, AB = 6 cm, AC = 5 cm and BD = 3 cm. Find DC.

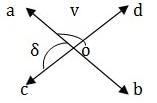
In the given figure, straight line AB and CD intersect at O. IF ∠δ =3∠v, then ∠v = ?
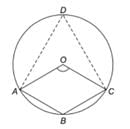
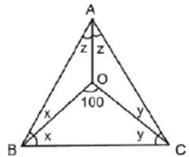
In a triangle ABC, the incentre is at 0. If ㄥBOC = 100°, find ㄥBAC.
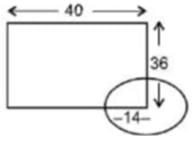
A rectangular enclosure 40 m x 36 m has a horse tethered to a corner with a rope of 14 m in length. What is the ratio of the respective areas it can graze if it is outside the enclosure and if it is inside the enclosure?
Read the passage below and solve the questions based on it.
The area of a square is equal to the area of a rectangle. Moreover, the perimeter of the square is also equal to the perimeter of the rectangle.
Q. The length of the rectangle is equal to the:
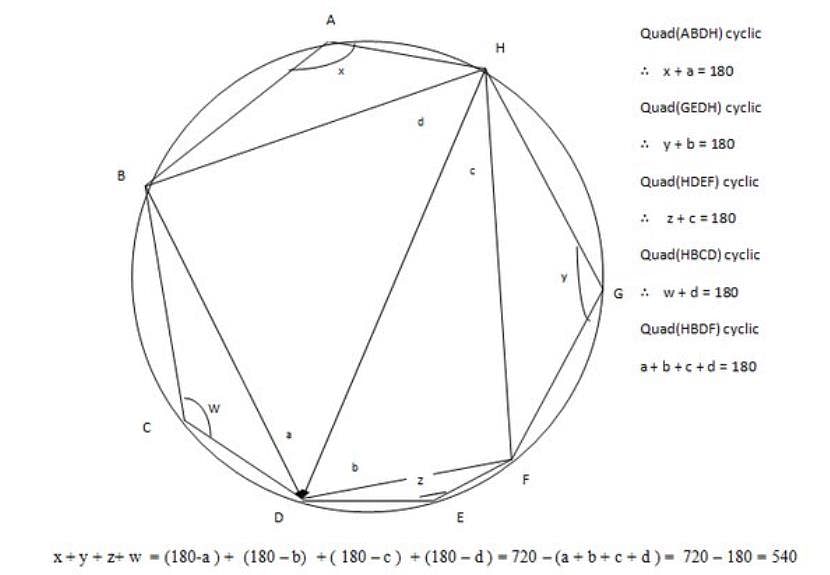
A quadrilateral is inscribed in a circle. If an angle is inscribed in each of the four segments outside the quadrilateral, then what is the sum of these four angles?
|
541 videos|681 docs|263 tests
|