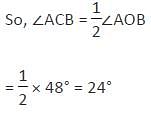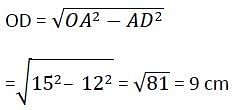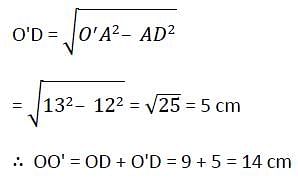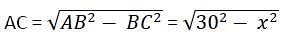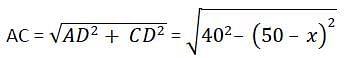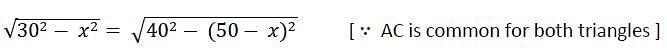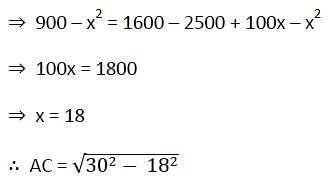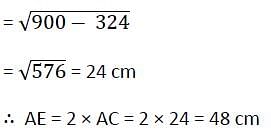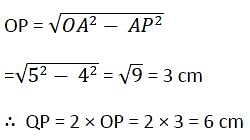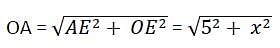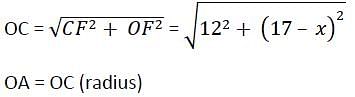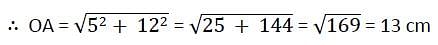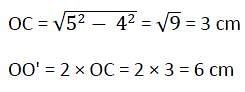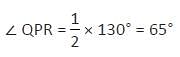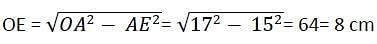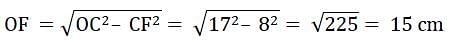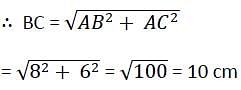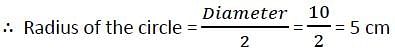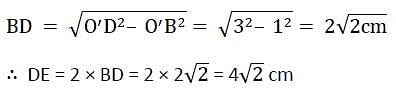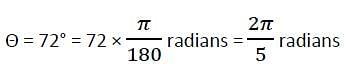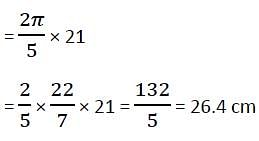MCQ: Circles - 2 - SSC CGL MCQ
15 Questions MCQ Test Quantitative Aptitude for SSC CGL - MCQ: Circles - 2
Directions: Kindly study the following questions carefully and choose the right answer:
In a right angled triangle, the circumcentre of the triangle lies.
Directions: Kindly study the following questions carefully and choose the right answer:
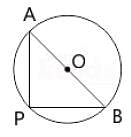
In the given figure below, ∠AOB = 48° and AC and OB intersect each other at right angles.
What is the measure of ∠OBC? (O is the centre of the circle)
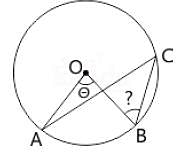
What is the measure of ∠OBC? (O is the centre of the circle)

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Directions: Kindly study the following questions carefully and choose the right answer:
The length of the common chord of two intersecting circles is 24 cm. If the diameter of the circles are 30 cm and 26 cm, then the distance between the centre (in cm) is
Directions: Kindly study the following questions carefully and choose the right answer:
A unique circle can always be drawn through x number of given non-collinear points, then x must be
Directions: Kindly study the following questions carefully and choose the right answer:
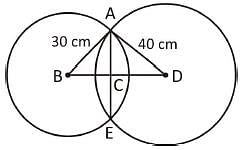
The length of the common chord of two circles of radii 30 cm and 40 cm whose centres are 50 cm apart, is (in cm)
Directions: Kindly study the following questions carefully and choose the right answer:
The distance betwen two parallel chords of length 8 cm each in a circle of diameter 10 cm is
Directions: Kindly study the following questions carefully and choose the right answer:
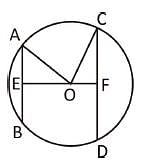
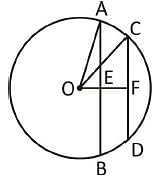
AB and CD are two parallel chords of a circle such that AB = 10 cm and CD = 24 cm. If the chords are on the opposite sides of the centre and distance between them is 17 cm, then the radius of the circle is :
Directions: Kindly study the following questions carefully and choose the right answer:
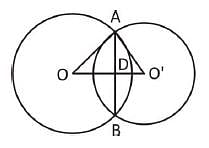
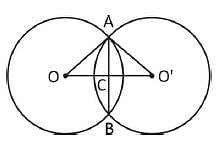
Two circles of same radius 5 cm, intersect each other at A and B. If AB = 8 cm, then the distance between the centre is :
Directions: Kindly study the following questions carefully and choose the right answer:
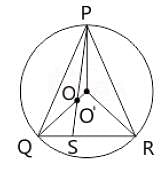
O and O' are respectively the orthocentre and circumcentre of an acute angled triangle PQR. the point P and O are joined and produced to meet the side QR at S. If ∠PQS = 60° and ∠QO'R = 130° then ∠RPS = ?
Directions: Kindly study the following questions carefully and choose the right answer:
In a circle of radius 17 cm, two parallel chords of length 30 cm and 16 cm are drawn. If both the chords are on the same side of the centre, then the distance between the chords is
Directions: Kindly study the following questions carefully and choose the right answer:
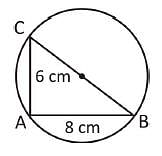
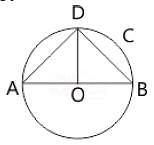
The length of two chords AB and AC of a circle are 8 cm and 6 cm and ∠BAC = 90°, then the radius of circle is
Directions: Kindly study the following questions carefully and choose the right answer:
Two circles touch each other internally. Their radii are 2 cm and 3 cm. The biggest chord of the greater circle which is outside the inner circle is of length
Directions: Kindly study the following questions carefully and choose the right answer:
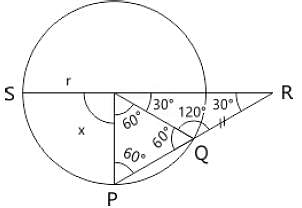
PQ is a chord of a circle with centre O and SOR is a line segment originating from a point S on the circle and intersecting PQ produced at R such that QR = OS. If ∠QRO = 30° then ∠POS = ?
Directions: Kindly study the following questions carefully and choose the right answer:
AB is the diameter of a circle with centre O and radius OD is perpendicular to AB. Find the angle BAD
Directions: Kindly study the following questions carefully and choose the right answer:
In a circle of radius 21 cm, an arc subtends an angle of 72° at the centre. The length of the arc is
|
314 videos|170 docs|185 tests
|
|
314 videos|170 docs|185 tests
|