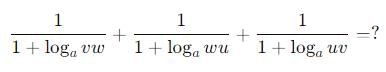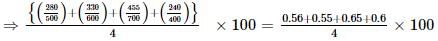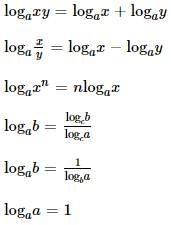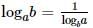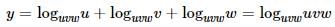GATE Numerical Ability Questions (Quant & Analytical) -2 - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - GATE Numerical Ability Questions (Quant & Analytical) -2
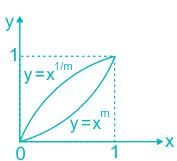
Select the graph that schematically represents BOTH y = xm and y = x1/m properly in the interval 0 ≤ x ≤ 1, for integer values of m, where m > 1.
It was estimated that 52 men can complete a strip in a newly constructed highway connecting cities P and Q in 10 days. Due to an emergency, 12 men were sent to another project. How many numbers of days, more than the original estimate, will be required to complete the strip?
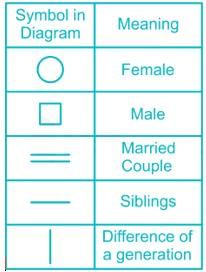
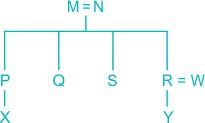
M and N had four children P, Q, R and S. Of them, only P and R were married. They had children X and Y respectively. If Y is a legitimate child of W, which one of the following statements is necessarily FALSE?
There are five levels {P, Q, R, S, T} in a linear supply chain before a product reaches customers, as shown in the figure.

At each of the five levels, the price of the product is increased by 25%. If the product is produced at level P at the cost of Rs. 120 per unit, what is the price paid (in rupees) by the customers?
Given that a and b are integers and a + a2 b3 is odd, which one of the following statements is correct?
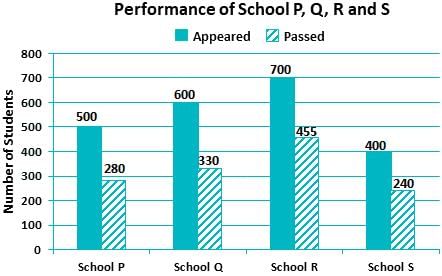
The bar graph shows the data of the students who appeared and passed in an examination for four school P, Q, R and S. The average of success rates (in percentage) of these four schools is _____.
A person divided an amount of Rs. 100,000 into two parts and invested in two different schemes. In one he got 10% profit and in the other he got 12%. If the profit percentages are interchanged with these investments he would have got Rs.120 less. Find the ratio between his investments in the two schemes.
Consider the following three statements:
(i) Some roses are red.
(ii) All red flowers fade quickly.
(iii) Some roses fade quickly.
Q. Which of the following statements can be logically inferred from the above statements?
A rectangle becomes a square when its length and breadth are reduced by 10 m and 5 m, respectively. During this process, the rectangle loses 650 m2 of area. What is the area of the original rectangle in square meters?
The value of the expression