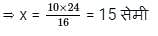Test: Circle & its chords (वृत्त और उसकी जीवाएँ) - Banking Exams MCQ
15 Questions MCQ Test Quantitative Aptitude/संख्यात्मक योग्यता - Test: Circle & its chords (वृत्त और उसकी जीवाएँ)
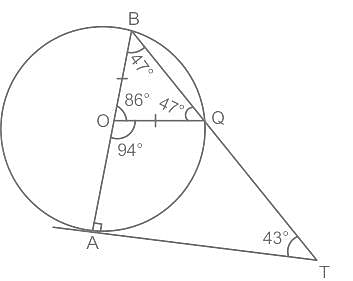
दी गई आकृति में AB केंद्र O वाले वृत्त का व्यास है और AT एक स्पर्श रेखा है, यदि ∠AOQ = 94° है, तो ∠ATQ कितना है?

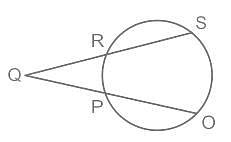
दिए गए चित्र में QR = 4 सेमी, QP = 8 सेमी, और OP = 12 सेमी है। QS का मान ज्ञात कीजिए।

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
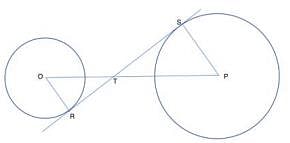
दी गई आकृति में, केंद्र O वाले वृत्त की त्रिज्या 10 सेमी है। केंद्र P वाले वृत्त की त्रिज्या x है। STR बिंदुओं R और S पर दोनों वृत्तों के लिए एक उभयनिष्ठ स्पर्शरेखा है जैसा कि चित्र में दर्शाया गया है। RT = 16 सेमी और TS = 24 सेमी है। x का मान (सेमी में) क्या है?

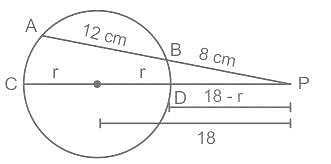
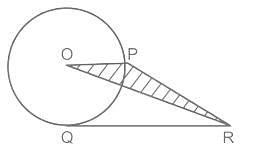
एक वृत्त की जीवा AB और व्यास CD, वृत्त के बाहर, बिंदु P पर मिलते हैं जब वृत्त का निर्माण होता है, यदि PB = 8 सेमी, AB = 12 सेमी और वृत्त के केंद्र से P की दूरी 18 सेमी है, तो वृत्त की त्रिज्या (सेमी में) किसके निकटतम है?
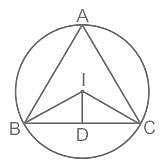
ΔABC के परिकेन्द्र I से BC पर लंब ID खींचा जाता है। यदि ∠BAC = 60°, तो ∠BID का मान है
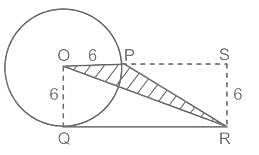
दिए गए चित्र में, O वृत्त का केंद्र है तो OP||QR है, QR वृत्त की स्पर्श-रेखा है और OP = 6 सेमी है, ∆OPR का क्षेत्रफल ज्ञात कीजिये।
दी गयी आकृति में ∠BOQ = 60° है और AB वृत्त का व्यास है। ∠ABO का मान ज्ञात कीजिये।
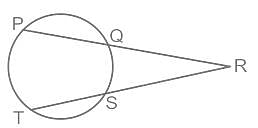
एक वृत्त में, जीवा PQ और TS को इस प्रकार बढ़ाया जाता है कि वे R पर मिलती हैं। यदि RQ = 14.4 सेमी, PQ = 11.2 सेमी, और SR = 12.8 सेमी है, तो जीवा TS की लम्बाई कितनी होगी?
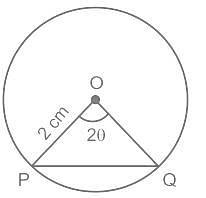
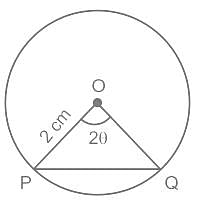
दी गई आकृति में OP और OQ केंद्र O वाले एक वृत्त की त्रिज्याएँ हैं। यदि त्रिज्या 2 सेमी है और यह केंद्र पर 2θ का कोण बनाती है, (θ< 45°)। जीवा PQ की लंबाई ज्ञात कीजिए।
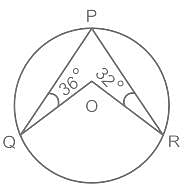
दी गयी आकृति में O वृत्त का केंद्र है। ∠PQO = 36° और ∠PRO = 32° है। ∠QOR का मान ज्ञात कीजिए।
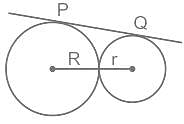
दो वृत्त बाह्यतः एक दूसरे को बिंदु X पर स्पर्श करते हैं। PQ दोनों वृत्तों के लिए सामान्य उभयनिष्ठ स्पर्श रेखा है जो वृत्तों को बिंदु P और बिंदु Q पर स्पर्श करती है। यदि वृत्तों की त्रिज्या R और r हैं, तब PQ2 ज्ञात कीजिये।
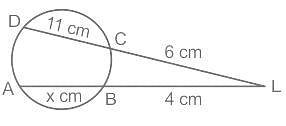
दी गई आकृति में, जीवा AB और CD बिंदु L पर एक दूसरे को प्रतिच्छेद करती हैं। AB की लंबाई ज्ञात कीजिए।
आरेख में, AD वृत्त की स्पर्श रेखा है और ABC छेदक रेखा है। यदि AB = 4 सेमी और BC = 5 सेमी है, तो AD की लंबाई_______है
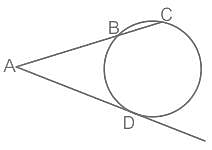
एक वृत्त त्रिभुज ΔABC के परिगत है। O वृत्त का केंद्र है और CP वृत्त के बिंदु C पर स्पर्शरेखा है। यदि BC, ∠OCP को द्विविभाजित करती है, तो ∠BAC का संपूरख कोण क्या है?
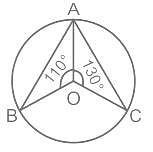
A, B और C एक वृत्त पर तीन बिंदु इस प्रकार है कि जीवा AB और AC द्वारा केंद्र O बना आंतरिक कोणक्रमशः 110° और 130° हैं। ∠BAC का मान है:
|
225 videos|9 docs|26 tests
|
|
225 videos|9 docs|26 tests
|