Test: Geometry (ज्यामिति) - Banking Exams MCQ
10 Questions MCQ Test Quantitative Aptitude/संख्यात्मक योग्यता - Test: Geometry (ज्यामिति)
एक त्रिभुज के शीर्ष (4, 1), (1, 1), (3, 5) है, तो वह होगा:
एक बहुभुज के आंतरिक कोणों का योगफल 1620° है। बहुभुज के भुजाओं की संख्या ज्ञात कीजिए।
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
समरूप त्रिभुज ΔPQR और ΔDEF की भुजाएं 5 ∶ 6 के अनुपात में हैं। यदि ΔPQR का क्षेत्रफल 75 सेमी2 के बराबर है तो ΔDEF का क्षेत्रफल क्या है?
उस त्रिभुज का क्षेत्रफल क्या है जिसके शीर्ष निर्देशांक (1, 2), (-4, -3) और (4, 1) द्वारा दिए गए हैं:
शब्द 'OX' के आखिरी वाले अक्षर द्वारा बनने वाले कोण की पहचान कीजिए।
यदि A अपने कोटिपूरक कोण से 26° अधिक है और B अपने संपूरक कोण से 30° कम है, तो (A - B) का मान ज्ञात कीजिए।
दी गई आकृति में, जीवा AB और CD बिंदु L पर एक दूसरे को प्रतिच्छेद करती हैं। AB की लंबाई ज्ञात कीजिए।

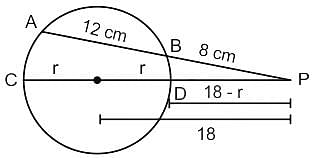
एक वृत्त की जीवा AB और व्यास CD, वृत्त के बाहर, बिंदु P पर मिलते हैं जब वृत्त का निर्माण होता है, यदि PB = 8 सेमी, AB = 12 सेमी और वृत्त के केंद्र से P की दूरी 18 सेमी है, तो वृत्त की त्रिज्या (सेमी में) किसके निकटतम है?
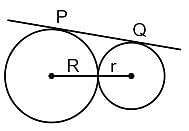
दो वृत्त बाह्यतः एक दूसरे को बिंदु X पर स्पर्श करते हैं। PQ दोनों वृत्तों के लिए सामान्य उभयनिष्ठ स्पर्श रेखा है जो वृत्तों को बिंदु P और बिंदु Q पर स्पर्श करती है। यदि वृत्तों की त्रिज्या R और r हैं, तब PQ2 ज्ञात कीजिये।
|
225 videos|9 docs|26 tests
|
|
225 videos|9 docs|26 tests
|