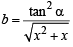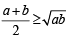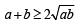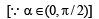JEE Advanced (Single Correct MCQs): Quadratic Equation and Inequalities (Inequalities) - JEE MCQ
30 Questions MCQ Test Chapter-wise Tests for JEE Main & Advanced - JEE Advanced (Single Correct MCQs): Quadratic Equation and Inequalities (Inequalities)
If ℓ, m, n are real, ℓ ≠ m, then the roots by the equation: (ℓ – m)x2 – 5 (ℓ + m) x – 2 (ℓ – m) = 0 are (1979)
The equation x + 2y + 2z = 1 and 2x + 4y + 4z = 9 have
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If x, y and z are real and different and (1979) u = x2 + 4y2 + 9z2 – 6yz – 3zx – 2xy, then u is always.
Let a > 0, b >0 and c > 0. Then the roots of the equation ax2 + bx + c = 0 (1979)
Both the roots of the equation (x – b) (x – c) + (x – a) (x – c) + (x – a) (x – b) = 0are always
The least value of the expression 2 log10x – logx(0.01), for x > 1, is(1980)
If (x2 + px + 1) is a factor of (ax3 + bx + c), then (1980)
The number of real solutions of the equation | x |2 – 3 | x | + 2 = 0 is (1982 - 2 Marks)
Two towns A and B are 60 km apart. A school is to be built to serve 150 students in town A and 50 students in town B. If the total distance to be travelled by all 200 students is to be as small as possible, then the school should be built at (1982 - 2 Marks)
If p, q, r are any real numbers, then (1982 - 2 Marks)
The largest interval for which x12 – x9 + x4 – x + 1 > 0 is (1982 - 2 Marks)
The equation 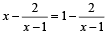 has (1984 - 2 Marks)
has (1984 - 2 Marks)
If a2 + b2 + c2 = 1, then ab + bc + ca lies in the interval (1984 - 2 Marks)
If log0.3 (x – 1) < log0.09(x – 1), then x lies in the interval – (1985 - 2 Marks)
If α and β are the roots of x2 + px + q = 0 and α4, β4 are the roots of x2 – rx + s = 0, then the equation x2 – 4qx + 2q2 – r = 0 has always (1989 - 2 Marks)
Let a, b, c be real numbers, a ≠ 0. If α is a r oot of a2x2 + bx + c = 0 . β is the root of a2x2 – bx – c = 0 and 0 < α < β, then the equation a2x2 + 2bx + 2c = 0 has a root g that always satisfies (1989 - 2 Marks)
The number of solutions of the equation sin(e)x = 5x + 5–x is (1990 - 2 Marks)
Let α, β be the roots of the equation (x – a) (x – b) = c, c ≠ 0.Then the roots of the equation (x – α) (x – β) + c = 0 are (1992 - 2 Marks)
The number of poin ts of intersection of two curves y = 2 sinx and y = 5x2 + 2x + 3 is (1994)
If p, q, r are +ve and are in A.P., the roots of quadratic equation px2 + qx + r = 0 are all real for (1994)
Let p,q ∈ {1,2, 3,4} . The number of equations of the form px2 + qx + 1 = 0 having real roots is (1994)
If the roots of the equation x2 – 2ax + a2 + a – 3 = 0 are real and less than 3, then (1999 - 2 Marks)
If α and β (α < β) are the roots of the equation x2 + bx + c = 0, where c < 0 < β, then (2000S)
If a, b, c, d are positive real numbers such that a + b + c + d = 2, then M = (a + b) (c + d) satisfies the relation
If b > a, then the equation (x – a) (x – b) –1 = 0 has (2000S)
For the equation 3x2 + px + 3 = 0, p > 0, if one of the root is square of the other, then p is equal to (2000S)
If a1,a2.....,an are positive real numbers whose product is a fixed number c, then the minimum value of a1 + a2 + .......+an-1 + 2an is (2002S)
The set of all real numbers x for which x2 – | x + 2 | + x > 0, is (2002S)
If 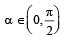 then
then 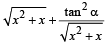 is always greater than or equal to (2003S)
is always greater than or equal to (2003S)
For all ‘x’, x2 + 2ax + 10– 3a > 0, then the interval in which ‘a’ lies is (2004S)
|
446 docs|930 tests
|
|
446 docs|930 tests
|


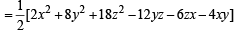
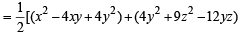
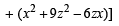
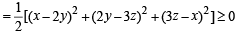
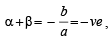
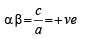
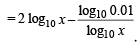
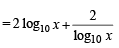
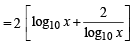
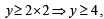
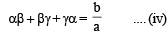


 (using γ = p = – c / a)
(using γ = p = – c / a)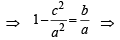 a2 – c2= ab
a2 – c2= ab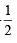 (p + q- |q - p|)
(p + q- |q - p|)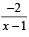 on both sides to get x = 1, but it is not possible. So given eq. has no roots.
on both sides to get x = 1, but it is not possible. So given eq. has no roots.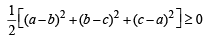
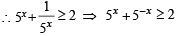
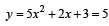
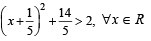
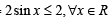
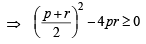 (∵ p, q, r are in A.P.)
(∵ p, q, r are in A.P.)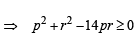
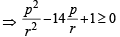
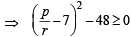
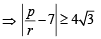
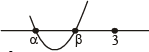
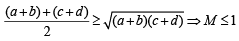

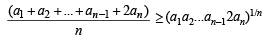
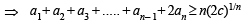
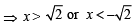
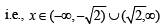
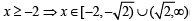 ....(2)
....(2)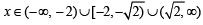
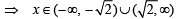
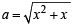 and
and