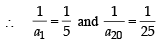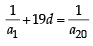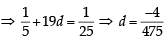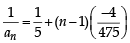JEE Advanced (Single Correct MCQs): Sequences and Series - JEE MCQ
19 Questions MCQ Test Chapter-wise Tests for JEE Main & Advanced - JEE Advanced (Single Correct MCQs): Sequences and Series
If x, y and z are pth, qth and rth terms respectively of an A.P. and also of a G.P., then xy – z yz – x zx – y is equal to :
The third term of a geometric progression is 4. The product of the first five terms is (1982 - 2 Marks)
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The rational number, which equals the number 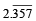 with recurring decimal is (1983 - 1 Mark)
with recurring decimal is (1983 - 1 Mark)
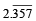 with recurring decimal is (1983 - 1 Mark)
with recurring decimal is (1983 - 1 Mark)If a, b, c are in G.P., then the equations ax 2 + 2bx + c = 0 and dx 2 + 2ex + f = 0 have a common root if 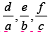 are in –– (1985 - 2 Marks)
are in –– (1985 - 2 Marks)
Sum of the first n terms of the series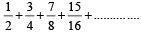 ....... is equal to (1988 - 2 Marks)
....... is equal to (1988 - 2 Marks)
The number log 2 7 is (1990 - 2 Marks)
If ln(a + c), ln (a – c), ln (a – 2b + c) are in A.P., then (1994)
Let a1, a2, ..... a10 be in A, P, and h1, h2,....h10 be in H.P. If a1 = h1 = 2 and a10 = h10 = 3, then a4h7 is (1999 - 2 Marks)
The harmonic mean of the roots of the equation 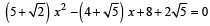 is (1999 - 2 Marks)
is (1999 - 2 Marks)
Consider an infinite geometric series with first term a and common ratio r. If its sum is 4 and the second term is 3/4, then (2000S)
Let α, β be the roots of x2 - x + p = 0 and γ, δ be the roots of x2 - 4x + q = 0. If α, β, γ, δ are in G.P., then the integral values of p and q respectively, are (2001S)
Let the positive numbers a, b, c, d be in A.P. Then abc, abd, acd, bcd are (2001S)
If the sum of the first 2n terms of the A.P. 2, 5, 8, …, is equal to the sum of the first n terms of the A.P. 57, 59, 61, …, then n equals(2001S)
Suppose a, b, c are in A.P. and a2, b2, c2 are in G.P. if a < b < c and a + b + c =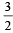 , then the value of a is (2002S)
, then the value of a is (2002S)
An infinite G.P. has first term ‘x’ and sum ‘5’, then x belongs to (2004S)
In the quadratic equation ax2 + bx + c = 0, Δ = b2 – 4ac and α + β, α2 + β2, α3 + β3, are in G.P. where α, β are the root of ax2 + bx + c = 0, then which of the following is correct
In the sum of first n terms of an A.P. is cn2, then the sum of squares of these n terms is (2009)
Let a1, a2, a3, ..... be in harmonic progression with a1 = 5 and a20 = 25. The least positive integer n for which an < 0 is (2012 )
Let bi > 1 for i = 1, 2, ..., 101. Suppose loge b1, loge b2, ...., loge b101 are in Arithmetic Progression (A.P.) with the common difference loge 2. Suppose a1, a2, ...., a101 are in A.P. such that a1= b1 and a51= b51. If t= b1+b2 + .... + b51 and s= a1+a2+ .... + a53, then (JEE Adv. 2016)
|
446 docs|930 tests
|
|
446 docs|930 tests
|


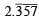 = 2 + .357 + 0.000357 + ...∞
= 2 + .357 + 0.000357 + ...∞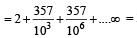
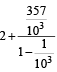
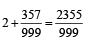
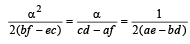
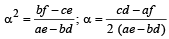
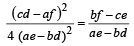
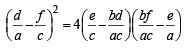
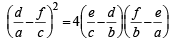 [Using eq. (1)]
[Using eq. (1)]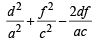
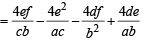
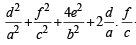
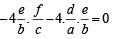
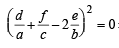
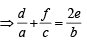
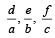 are in A.P..
are in A.P..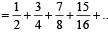 n terms
n terms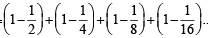 ..n terms
..n terms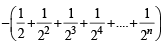
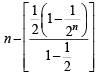 = n - 1+2-n
= n - 1+2-n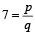 (a rational number)
(a rational number)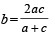
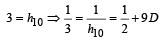
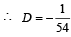
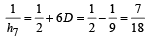
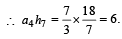
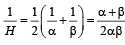
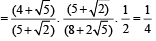
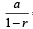 = 4 and ar = 3 /4 ⇒
= 4 and ar = 3 /4 ⇒ 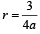
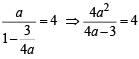
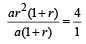 ⇒
⇒ 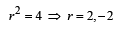
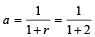 or
or 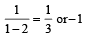
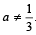 Hence a = -1 and r = -2.
Hence a = -1 and r = -2.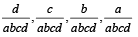 are also in A.P..
are also in A.P..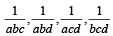 are in A.P..
are in A.P..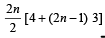
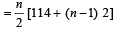
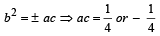
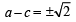
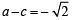 ....(2)
....(2)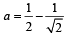
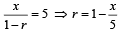
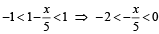
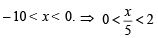
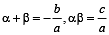




 are in G.P.
are in G.P. are in G.P.
are in G.P.

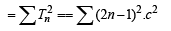
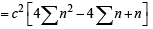
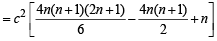
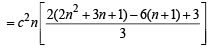
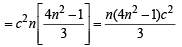
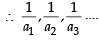 .. are in A.P..
.. are in A.P..