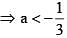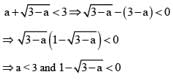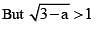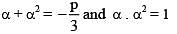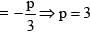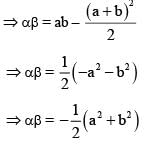JEE Advanced Level Test: Quadratic Equation- 2 - JEE MCQ
30 Questions MCQ Test Chapter-wise Tests for JEE Main & Advanced - JEE Advanced Level Test: Quadratic Equation- 2
The first and last term of an A.P. are 1 and 11. If the sum of its terms is 36, then the number of terms will be
Let two numbers have arithmetic mean 9 and geometric mean 4. Then these numbers are the roots of the quadratic equation
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If ‘l’ is one of the roots of ax2 + 3x + 5 = 0 then the second root is
If the product of the roots of the equation 5x2 - 4x + 2 + k (4x2 - 2x - 1) = 0 is 2 then k =
If the equations x2 + ax + b = 0 and x2 + bx + a = 0 (a ≠ b) have a common root then a + b =
If 2x – 7 – 5x2 has maximum value at x = a then a =
Number of real roots of the equation 3x2 + 4 | x | +5 = 0 are
If a and b are the roots of x2 – 2x + 4 = 0 then the value of α6 + β6 is
If α + β = –2 and α3 + β3 = -56 then the quadratic equation whose roots are α, β is
tan 22o and tan 23o are roots of x2 + ax + b = 0 then
The value of ‘a’ for which one root of the quadratic equation (a2 – 5a + 3) x2 – (3a – 1) x + 2 = 0 is twice as large as other is
Two students while solving a quadratic equation in x, one copied the constant term incorrectly and got the roots as 3 and 2. The other copied correctly the constant term and coefficient of x2 as -6 and 1 respectively. The correct roots are
If one root of the equation ax2 + bx + c = 0 is the square of the other, then
The roots of the equation ax2 + bx + c = 0, a ∈ R+, are two consecutive odd positive integers. Then
If a + b + c = 0 then the equation 3ax2 + 2bx + c = 0 has
The value of ‘a’ if relation (a – 1)x2 – (a2 – 3a + 2) x + a2 – 1 = 0 is satisfied for more than two values of x, is :
If the roots of (x - α) (x - β) = λ are γ and δ, then the roots of (x - γ) (x - δ) + λ = 0
If the roots of a (b - c) x2 + b (c - a) x +c (a - b) = 0 are equal, then a, b, c are in :
The least value of the sum of the squares of the roots of the equation x2 – (a – 2) x – a – 1 = 0 is:
The set of values of p for which both roots of the equation 3x2 + 2x + p(p – 1) = 0 are of opposite sign is:
If each pair of equations x2 + ax + b = 0, x2 + bx + c = 0 and x2 + cx + a = 0 has a common root then product of all common roots is :
The equation (x2 + 6x + 7)2 + 6 (x2 + 6x + 7) + 7 = x has
Let S be the set of values of ‘a’ for which 2 lies between the roots of quadratic equation x2 + (a + 2) x a – 3 = 0. Then S is given by:
The values of a for which one root is greater than 1 and the other root less than zero, of the equation x2 + (2a + 1) x + (a – 1) = 0 is :
If both the roots of (x – a) (x – 20) + 1 = 0 are integers (a ∈ I) then the number of value of a is
If p and q are the roots of x2 + px + q = 0. Then:
If the roots of the equation x2 - 2ax + a2 + a - 3 = 0 are real less than 3, then:
For the equation 3x2 + px + 3 = 0, p > 0, if one of the roots is square of the other, then p is equal to :
If the roots of the equation are equal in magnitude but opposite in sign, then their product is :
|
446 docs|930 tests
|
|
446 docs|930 tests
|


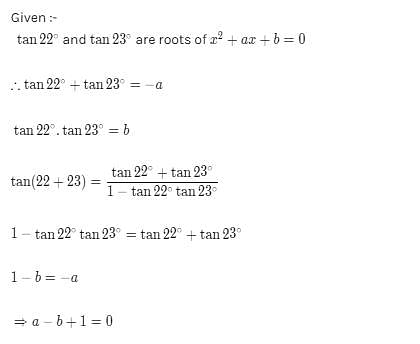

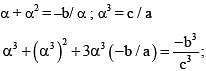
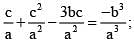
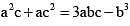
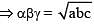
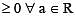
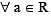
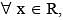 then
then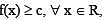 hence b - a2 > c
hence b - a2 > c