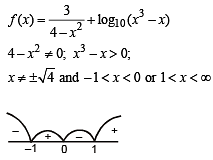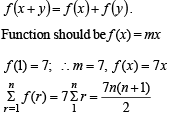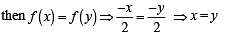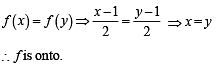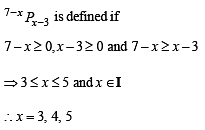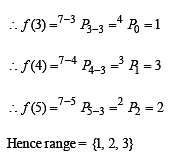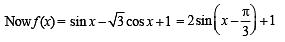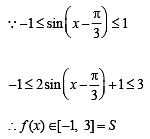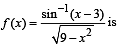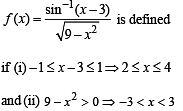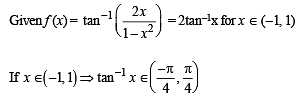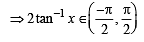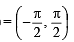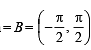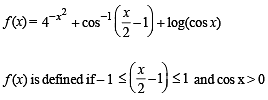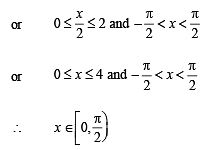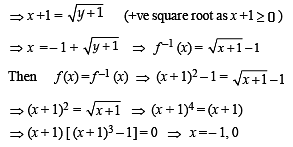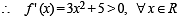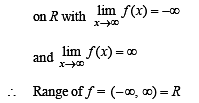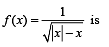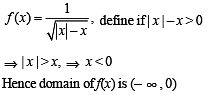Test: JEE Main 35 Year PYQs: Functions - JEE MCQ
17 Questions MCQ Test Chapter-wise Tests for JEE Main & Advanced - Test: JEE Main 35 Year PYQs: Functions
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If f : R → R satisfies f (x + y) = f ( x) + f (y) , for all x, 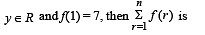
A function f from the set of natural numbers to integers defined by
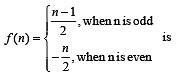
The range of the function f (x) = 7- x Px -3 is
If f : R → S, defined by
f (x) = sin x - √3 cosx+ 1, is onto, then the interval of S is
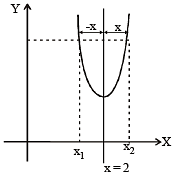
The graph of the function y = f(x) is symmetrical about the line x = 2, then
L et f : (– 1, 1) → B , be a function defined by 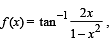 then f is both one - one and onto when B is the interval
then f is both one - one and onto when B is the interval
A function is matched below against an interval where it is supposed to be increasing. Which of the following pairs is incorrectly matched?

A real valued function f(x) satisfies the functional equation f(x – y) = f(x) f(y) – f(a – x) f(a + y) where a is a given constant and f(0) = 1, f(2a – x) is equal to
The largest interval lying in 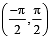 for which the function,
for which the function, 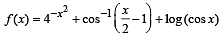 , is defined, is
, is defined, is
Let f: N→Y be a function defined as f(x) = 4x + 3 where Y = {y ∈ N : y = 4x + 3 for some x ∈ N}.
Show that f is invertible and its inverse is
Let f(x) = ( x + 1)2 – 1,x > –1
Statement -1 : The set {x : f(x) = f –1(x) = {0, –1}
Statement-2 : f is a bijection.
|
446 docs|930 tests
|
|
446 docs|930 tests
|