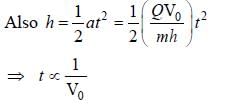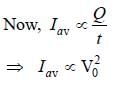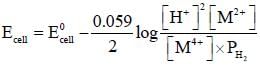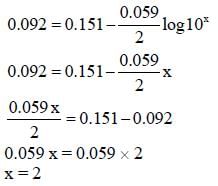JEE (Advanced) 2016 Paper - 2 with Solutions - JEE MCQ
30 Questions MCQ Test National Level Test Series for JEE Advanced 2025 - JEE (Advanced) 2016 Paper - 2 with Solutions
Q. No. 1 -6 carry 3 marks each.
Each question has FOUR options (A), (B), (C) and (D). ONLY ONE of these four options is correct.
Q.
The electrostatic energy of Z protons uniformly distributed throughout a spherical nucleus of radius R is
given by
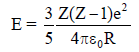
The measured masses of the neutron 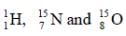 are 1.008665 u, 1.007825 u, 15.000109 u and 15.003065u, respectively. Given that the radii of both the
are 1.008665 u, 1.007825 u, 15.000109 u and 15.003065u, respectively. Given that the radii of both the 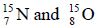 nuclei are same, 1 u = 931.5 MeV/c2 (c is the speed of light) and e2 /(4πε0) = 1.44 MeV fm. Assuming that the difference between the binding energies of
nuclei are same, 1 u = 931.5 MeV/c2 (c is the speed of light) and e2 /(4πε0) = 1.44 MeV fm. Assuming that the difference between the binding energies of 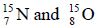 is purely due to the electrostatic energy, the radius of either of the nuclei is (1 fm = 10-15m)
is purely due to the electrostatic energy, the radius of either of the nuclei is (1 fm = 10-15m)
given by
The measured masses of the neutron
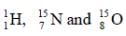 are 1.008665 u, 1.007825 u, 15.000109 u and 15.003065u, respectively. Given that the radii of both the
are 1.008665 u, 1.007825 u, 15.000109 u and 15.003065u, respectively. Given that the radii of both the The ends Q and R of two thin wires, PQ and RS, are soldered (joined) together. Initially each of the wires has a length of 1 m at 100C. Now the end P is maintained at 100C, while the end S is heated and maintained at 4000C. The system is thermally insulated from its surroundings. If the thermal conductivity of wire PQ is twice that of the wire RS and the coefficient of linear thermal expansion of PQ is 1.2 x 10-5 K-1, the change in length of the wire PQ is
An accident in a nuclear laboratory resulted in deposition of a certain amount of radioactive material of half-life 18 days inside the laboratory. Tests revealed that the radiation was 64 times more than the permissible level required for safe operation of the laboratory. What is the minimum number of days after which the laboratory can be considered safe for use?
There are two Vernier calipers both of which have 1 cm divided into 10 equal divisions on the main scale. The Vernier scale of one of the calipers (C1) has 10 equal divisions that correspond to 9 main scale divisions. The Vernier scale of the other caliper (C2) has 10 equal divisions that correspond to 11 main scale divisions. The readings of the two calipers are shown in the figure. The measured values (in cm) by calipers C1 and C2 respectively, are
A gas is enclosed in a cylinder with a movable frictionless piston. Its initial thermodynamic state at pressure Pi = 105 Pa and volume Vi = 10-3 m3 changes to a final state at Pf = (1/32) x 105 Pa and Vf = 8 x 10-3 m3 in an adiabatic quasi-static process, such that P3V5 = constant. Consider another thermodynamic process that brings the system from the same initial state to the same final state in two steps: an isobaric expansion at Pi followed by an isochoric (isovolumetric) process at volume Vf. The amount of heat supplied to the system in the two-step process is approximately
A small object is placed 50 cm to the left of a thin convex lens of focal length 30 cm. A convex spherical mirror of radius of curvature 100 cm is placed to the right of the lens at a distance of 50 cm. The mirror is tilted such that the axis of the mirror is at an angle θ = 300 to the axis of the lens, as shown in the figure.
If the origin of the coordinate system is taken to be at the centre of the lens, the coordinates (in cm) of the
point (x, y) at which the image is formed are
Q.No. - 7 - 14 carry 4 marks each
Each questions has FOUR options (A), (B), (C) and (D). ONE OR MORE THAN ONE of these four option(s) is(are) correct.
Q.
While conducting the Young’s double slit experiment, a student replaced the two slits with a large opaque plate in the x-y plane containing two small holes that act as two coherent point sources (S1, S2) emitting light of wavelength 600 nm. The student mistakenly placed the screen parallel to the x-z plane (for z > 0) at a distance D = 3 m from the mid-point of S1S2, as shown schematically in the figure. The distance between the sources d = 0.6003 mm. The origin O is at the intersection of the screen and the line joining S1S2. which of the following is(are) true of the intensity pattern on the screen?
In an experiment to determine the acceleration due to gravity g, the formula used for the time period of a periodic motion is The values of R and r are measured to be (60
1) mm and (10
1) mm, respectively. In five successive measurements, the time period is found to be 0.52 s, 0.56 s, 0.57 s, 0.54 s and 0.59s. The least count of the watch used for the measurement of time period is 0.01 s. Which of the following statement(s) is(are) true?
A rigid wire loop of square shape having side of length L and resistance R is moving along the x-axis with a constant velocity v0 in the plane of the paper. At t = 0, the right edge of the loop enters a region of length 3L where there is a uniform magnetic field B0 into the plane of the paper, as shown in the figure. For sufficiently large v0, the loop eventually crosses the region. Let x be the location of the right edge of the loop. Let v(x), I(x) and F(x) represent the velocity of the loop, current in the loop, and force on the loop, respectively, as a function of x. Counter-clockwise current is taken as positive.
Which of the following schematic plot(s) is(are) correct? (Ignore gravity)
Light of wavelength λph falls on a cathode plate inside a vacuum tube as shown in the figure. The work function of the cathode surface is φ and the anode is a wire mesh of conducting material kept at a distance d from the cathode. A potential difference V is maintained between the electrodes. If the minimum de Broglie wavelength of the electrons passing through the anode is λe, which of the following statement(s) is(are) true?
Two thin circular discs of mass m and 4m, having radii of a and 2a, respectively, are rigidly fixed by a massless, rigid rod of length a through their centers. This a
ssembly is laid on a firm and flat surface, and set rolling without slipping on the surface so that the angular speed about the axis of the rod is ω. The angular momentum of the entire assembly about the point ‘O’ is(see the figure). Which of the following statement(s) is(are) true?
Consider two identical galvanometers and two identical resistors with resistance R. If the internal resistance of the galvanometers RC < R/2, which of the following statement(s) about any one of the galvanometers is(are) true?
In the circuit shown below, the key is pressed at time t = 0. Which of the following statement(s) is (are) true?
A block with mass M is connected by a massless spring with stiffness constant k to a rigid wall and moves without friction on a horizontal surface. The block oscillates with small amplitude A about an equilibrium position x0. Consider two cases: (i) when the block is at x0 ; and (ii) when the block is at x = x0 + A. In both the cases, a particle with mass m (< M) is softly placed on the block after which they stick to each other. Which of the following statement(s) is (are) true about the motion after the mass m is placed on the mass M?
Q. No. 15 -18 carry 3 marks each.
This section contains TWO paragraphs
Based on each paragraph, there are TWO questions
Each question has FOUR options (A), (B), (C) and (D). ONLY ONE of these four options is correct
Pragraph 1
A frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of a non-inertial frame of reference. The relationship between the force experienced by a particle of mass m moving on the rotating disc and the force
experienced by the particle in an inertial frame of reference is
where is the velocity of the particle in the rotating frame of reference and
is the position vector of the
particle with respect to the centre of the disc. Now consider a smooth slot along a diameter of a disc of radius R rotating counter-clockwise with a constant angular speed ω about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis . A small block of mass m is gently placed in the slot at
and is constrained to move only along the slot.
Q. The distance r of the block at time t is
Pragraph 1
A frame of reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity ω is an example of a non-inertial frame of reference. The relationship between the force experienced by a particle of mass m moving on the rotating disc and the force
experienced by the particle in an inertial frame of reference is
where is the velocity of the particle in the rotating frame of reference and
is the position vector of the
particle with respect to the centre of the disc. Now consider a smooth slot along a diameter of a disc of radius R rotating counter-clockwise with a constant angular speed ω about its vertical axis through its center. We assign a coordinate system with the origin at the center of the disc, the x-axis along the slot, the y-axis perpendicular to the slot and the z-axis along the rotation axis . A small block of mass m is gently placed in the slot at
and is constrained to move only along the slot.
Q.
The net reaction of the disc on the block is
Pragraph 2
Consider an evacuated cylindrical chamber of height h having rigid conducting plates at the ends and an insulating curved surface as shown in the figure. A number of spherical balls made of a light weight and soft material and coated with a conducting material are placed on the bottom plate. The balls have a radius r << h. Now a high voltage source (HV) is connected across the conducting plates such that the bottom plate is at +V0 and the top plate at –V0. Due to their conducting surface, the balls will get charged, will become equipotential with the plate and are repelled by it. The balls will eventually collide with the top plate, where the coefficient of restitution can be taken to be zero due to the soft nature of the material of the balls. The electric field in the chamber can be considered to be that of a parallel plate capacitor. Assume that there are no collisions between the balls and the interaction between them is negligible. (Ignore gravity)
Q. Which one of the following statements is correct?
Pragraph 2
Consider an evacuated cylindrical chamber of height h having rigid conducting plates at the ends and an insulating curved surface as shown in the figure. A number of spherical balls made of a light weight and soft material and coated with a conducting material are placed on the bottom plate. The balls have a radius r << h. Now a high voltage source (HV) is connected across the conducting plates such that the bottom plate is at +V0 and the top plate at –V0. Due to their conducting surface, the balls will get charged, will become equipotential with the plate and are repelled by it. The balls will eventually collide with the top plate, where the coefficient of restitution can be taken to be zero due to the soft nature of the material of the balls. The electric field in the chamber can be considered to be that of a parallel plate capacitor. Assume that there are no collisions between the balls and the interaction between them is negligible. (Ignore gravity)
Q. The average current in the steady state registered by the ammeter in the circuit will be
Q. No. 19 - 24 carry 3 marks each.
Each question has FOUR options (A), (B), (C) and (D). ONLY ONE of these four options is correct.
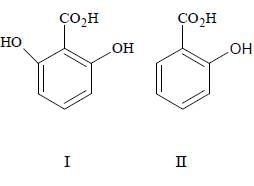
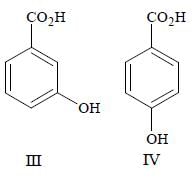
Q. The correct order of acidity for the following compounds is
The geometries of the ammonia complexes of Ni2+, Pt2+ and Zn2+, respectively, are
For the following electrochemical cell at 298 K,
Pt(s) | H2 (g, 1 bar) | H+ (aq, 1M) || M4+ (aq), M2+ (aq) | Pt(s)
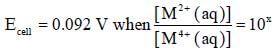
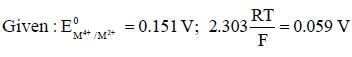
The value of x is
The major product of the following reaction sequence is
In the following reaction sequence in aqueous solution, the species X, Y and Z, respectively, are
The qualitative sketches I, II and III given below show the variation of surface tension with molar concentration of three different aqueous solutions of KCl, CH3OH and CH3(CH2)11 OSO3-Na+ at room temperature. The correct assignment of the sketches is
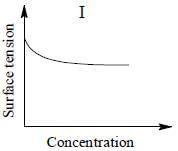
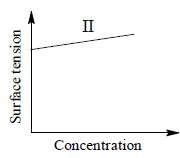
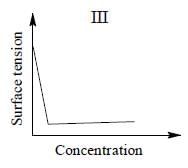
Q. No. 25 - 32 carry 4 marks each.
Each question has FOUR options (A), (B), (C) and (D). ONE OR MORE THAN ONE of these four
option(s) is(are) correct.
Q.
For ‘invert sugar’, the correct statement(s) is(are) (Given: specific rotations of (+)-sucrose, (+)-maltose, L-(–)-glucose and L-(+)-fructose in aqueous solution are +66º, +140º, –52º and +92º, respectively)
Among the following, reaction(s) which gives(give) tert-butyl benzene as the major product is(are)
Extraction of copper from copper pyrite (CuFeS2) involves
The CORRECT statement(s) for cubic close packed (ccp) three dimensional structure is(are)
Reagent(s) which can be used to bring about the following transformation is(are)
Mixture (s) showing positive deviation from Raoult’s law at 35oC is (are)
|
3 videos|2 docs|40 tests
|
|
3 videos|2 docs|40 tests
|


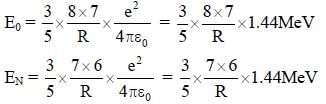
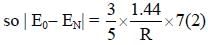 .........(i)
.........(i)
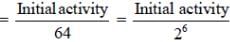

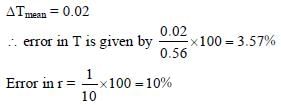
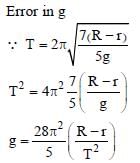
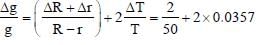


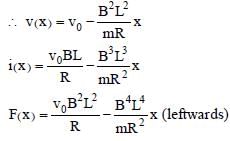
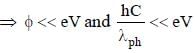
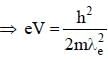
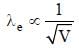
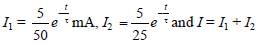
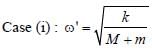
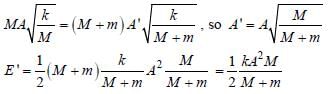
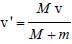
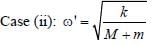
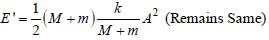
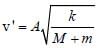
 is charge on ball then Q ∝ V0 .....(i)
is charge on ball then Q ∝ V0 .....(i)