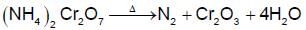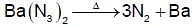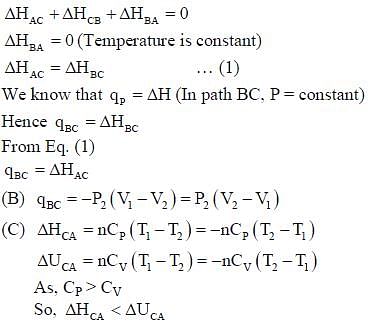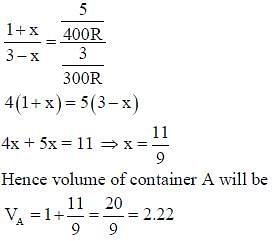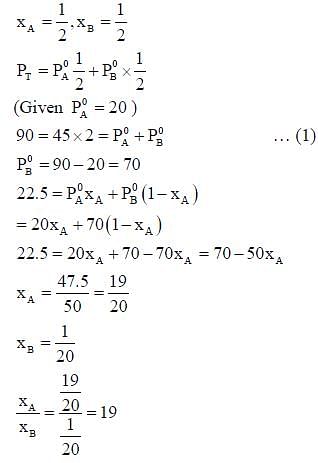JEE (Advanced) 2018 Paper - 1 - JEE MCQ
30 Questions MCQ Test National Level Test Series for JEE Advanced 2025 - JEE (Advanced) 2018 Paper - 1
The potential energy of a particle of mass m at a distance r from a fixed point O is given by V (r) = kr2/2,where k is a positive constant of appropriate dimensions. This particle is moving in a circular orbit of radiusR about the point O. If v is the speed of the particle and L is the magnitude of its angular momentum aboutO, which of the following statements is (are) true?
Consider a body of mass 1.0 kg at rest at the origin at time t = 0. A force 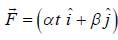 is applied on the body, where
is applied on the body, where 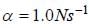 and
and 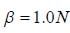 . The torque acting on the body about the origin at time
. The torque acting on the body about the origin at time 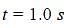
 . Which of the following statements is (are) true?
. Which of the following statements is (are) true?
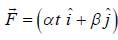 is applied on the body, where
is applied on the body, where 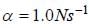 and
and 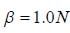 . The torque acting on the body about the origin at time
. The torque acting on the body about the origin at time 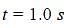
 . Which of the following statements is (are) true?
. Which of the following statements is (are) true?| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A uniform capillary tube of inner radius r is dipped vertically into a beaker filled with water. The water
rises to a height h in the capillary tube above the water surface in the beaker. The surface tension of water is σ. The angle of contact between water and the wall of the capillary tube is θ. Ignore the mass of water in the meniscus. Which of the following statements is (are) true?
rises to a height h in the capillary tube above the water surface in the beaker. The surface tension of water is σ. The angle of contact between water and the wall of the capillary tube is θ. Ignore the mass of water in the meniscus. Which of the following statements is (are) true?
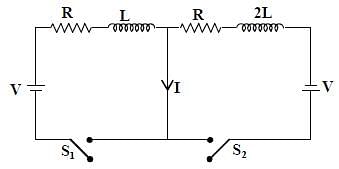
In the figure below, the switches S1 and S2 are
closed simultaneously at t = 0 and a current starts to
flow in the circuit. Both the batteries have the same
magnitude of the electromotive force (emf) and the
polarities are as indicated in the figure. Ignore
mutual inductance between the inductors. The
current I in the middle wire reaches its maximum
magnitude Imax at time 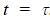 . Which of the
. Which of the
following statements is (are) true?
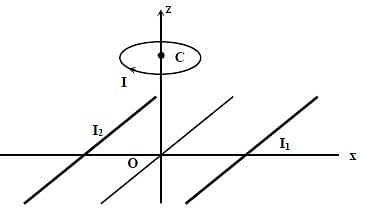
Two infinitely long straight wires lie in the xy-plane along the lines x = ±R. The wire located at x = +R
carries a constant current I1 and the wire located at x = –R carries a constant current I2. A circular loop of radius R is suspended with its centre at (0, 0, √3R ) and in a plane parallel to the xy-plane. This loop carries a constant current I in the clockwise direction as seen from above the loop. The current in the wire is taken to be positive if it is in the + ˆj direction. Which of the following statements regarding the magnetic field  is (are) true?
is (are) true?
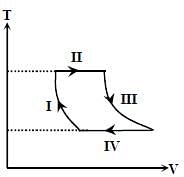
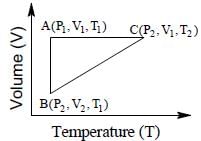
One mole of a monatomic ideal gas undergoes a cyclic process as shown in the figure (where V is the volume and T is the temperature). Which of the statements below is (are) true?
Two vectors 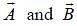 are defined as
are defined as 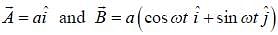 , where a is a constant and
, where a is a constant and  at time t =
at time t = 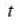 for the first time, the value of
for the first time, the value of 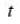 , in seconds, is _____.
, in seconds, is _____.
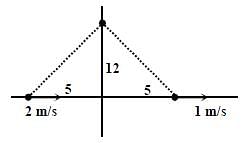
Two men are walking along a horizontal straight line in the same direction. The man in front walks at a
speed 1.0 ms −1 and the man behind walks at a speed 2.0 ms−1. A third man is standing at a height 12 m above the same horizontal line such that all three men are in a vertical plane. The two walking men are blowing identical whistles which emit a sound of frequency 1430 Hz. The speed of sound in air is 330 ms−1 At the instant, when the moving men are 10 m apart, the stationary man is equidistant from them. The frequency of beats in Hz, heard by the stationary man at this instant, is __________.
A ring and a disc are initially at rest, side by side, at the top of an inclined plane which makes an angle 60° with the horizontal. They start to roll without slipping at the same instant of time along the shortest path. If the time difference between their reaching the ground is 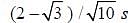 , then the height of the top of the inclined plane, in metres, is __________. Take g = 10 ms–2.
, then the height of the top of the inclined plane, in metres, is __________. Take g = 10 ms–2.
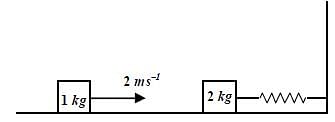
A spring-block system is resting on a frictionless floor as shown in the figure. The spring constant is 2.0 N m−1 and the mass of the block is 2.0 kg. Ignore the mass of the spring. Initially the spring is in an unstretched condition. Another block of mass 1.0 kg moving with a speed of 2.0 m s−1 collides elastically with the first block. The collision is such that the 2.0 kg block does not hit the wall. The distance, in metres, between the two blocks when the spring returns to its unstretched position for the first time after the collision is _________.
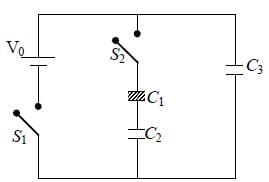
Three identical capacitors C1 , C2 and C3 have a capacitance of 1.0 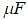 each and they are uncharged initially. They are connected in a circuit as shown in the figure and C1 is then filled completely with a dielectric material of relative permittivity
each and they are uncharged initially. They are connected in a circuit as shown in the figure and C1 is then filled completely with a dielectric material of relative permittivity 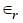 . The cell electromotive force (emf) V0 = 8V. First the switch S1 is closed while the switch S2 is kept open. When the capacitor C3 is fully charged, S1 is opened and S2 is closed simultaneously. When all the capacitors reach equilibrium, the charge on C3 is found to be
. The cell electromotive force (emf) V0 = 8V. First the switch S1 is closed while the switch S2 is kept open. When the capacitor C3 is fully charged, S1 is opened and S2 is closed simultaneously. When all the capacitors reach equilibrium, the charge on C3 is found to be 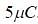 The value of
The value of 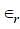 =_________.
=_________. 
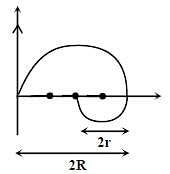
In the xy-plane, the region y > 0 has a uniform magnetic field B1 kˆ and the region y < 0 has another uniform magnetic field B2 kˆ. A positively charged particle is projected from the origin along the positive y-axis with speed 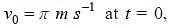 as shown in the figure. Neglect gravity in this problem. Let t = T be the time when the particle crosses the x-axis from below for the first time. If B2 = 4B1 , the average speed of the particle, in ms–1 , along the x-axis in the time interval T is __________.
as shown in the figure. Neglect gravity in this problem. Let t = T be the time when the particle crosses the x-axis from below for the first time. If B2 = 4B1 , the average speed of the particle, in ms–1 , along the x-axis in the time interval T is __________.
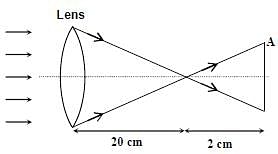
Sunlight of intensity 1.3 kWm–2 is incident normally on a thin convex lens of focal length 20 cm. Ignore
the energy loss of light due to the lens and assume that the lens aperture size is much smaller than its focal length. The average intensity of light, in kW m–2, at a distance 22 cm from the lens on the other side is __________.
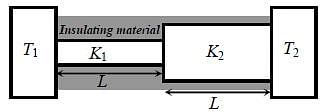
Two conducting cylinders of equal length but different radii are connected in series between two heat baths kept at temperatures T1= 300 K and T2 = 100 K, as shown in the figure. The radius of the bigger cylinder is twice that of the smaller one and the thermal conductivities of the materials of the smaller and the larger cylinders are K1 and K2 respectively. If the temperature at the junction of the two cylinders in the steady state is 200 K, then K1 / K2 =__________.
Consider the ratio 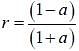 to be determined by measuring a dimensionless quantity a. If the error in the measurement of a is
to be determined by measuring a dimensionless quantity a. If the error in the measurement of a is 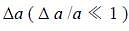 , then what is the error Δr in determining r ?
, then what is the error Δr in determining r ?
In an experiment the initial number of radioactive nuclei is 3000. It is found that 1000 ± 40 nuclei decayed in the first 1.0s. For |x| ≪ 1, ln(1 + x) = x up to first power in x . The error 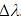 , in the determination of the decay constant
, in the determination of the decay constant 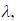 in s–1, is
in s–1, is
The compound(s) which generate(s) N2 gas upon thermal decomposition below 300°C is (are)
The correct statement(s) regarding the binary transition metal carbonyl compounds is (are)
(Atomic numbers: Fe = 26, Ni = 28)
B ased on the compounds of group 15 elements, the correct statement(s) is (are)
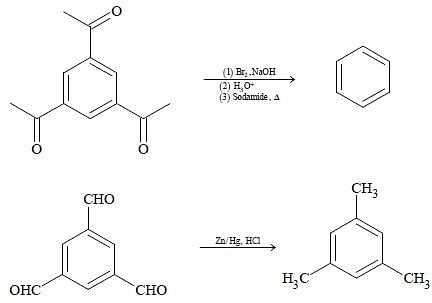
In the following reaction sequence, the correct structure(s) of X is (are)
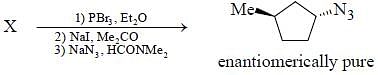
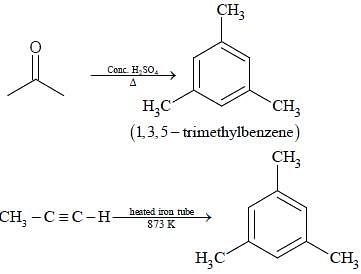
The reaction(s) leading to the formation of 1,3,5-trimethylbenzene is(are)
A reversible cyclic process for an ideal gas is shown below. Here, P, V, and T are pressure, volume and
temperature, respectively. The thermodynamic parameters q, w, H and U are heat, work, enthalpy and
internal energy, respectively.
The correct option(s) is (are)
Among the species given below, the total number of diamagnetic species is ___.
H atom, NO2 monomer, O2 − (superoxide), dimeric sulphur in vapour phase, Mn3O4, (NH4)2[FeCl4], (NH4)2[NiCl4], K2MnO4, K2CrO4
The ammonia prepared by treating ammonium sulphate with calcium hydroxide is completely used by
NiCl2.6H2O to form a stable coordination compound. Assume that both the reactions are 100% complete. If 1584 g of ammonium sulphate and 952 g of NiCl2.6H2O are used in the preparation, the combined weight (in grams) of gypsum and the nickel-ammonia coordination compound thus produced is ____.
(Atomic weights in g mol–1 : H = 1, N = 14, O = 16, S = 32, Cl = 35.5, Ca = 40, Ni = 59)
Consider an ionic solid MX with NaCl structure. Construct a new structure (Z) whose unit cell is
constructed from the unit cell of MX following the sequential instructions given below. Neglect the charge
balance.
(i) Remove all the anions (X) except the central one
(ii) Replace all the face centered cations (M) by anions (X)
(iii) Remove all the corner cations (M)
(iv) Replace the central anion (X) with cation (M)
The value of 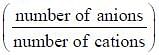 in Z is _______ .
in Z is _______ .
F or the electrochemical cell,
Mg(s) | Mg2+ (aq, 1 M) || Cu2+ (aq, 1 M) | Cu(s) the standard emf of the cell is 2.70 V at 300 K. When the concentration of Mg2+ is changed to x M, the cell potential changes to 2.67 V at 300 K. The value of x is ______.
(given, = 11500 K V−1, where F is the Faraday constant and R is the gas constant, ln(10) = 2.30)
= 11500 K V−1, where F is the Faraday constant and R is the gas constant, ln(10) = 2.30)
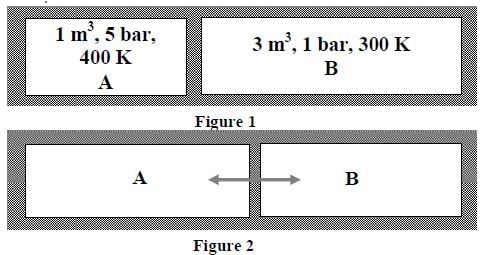
A closed tank has two compartments A and B, both filled with oxygen (assumed to be ideal gas). The
partition separating the two compartments is fixed and is a perfect heat insulator (Figure 1). If the old
partition is replaced by a new partition which can slide and conduct heat but does NOT allow the gas to
leak across (Figure 2), the volume (in m3) of the compartment A after the system attains equilibrium is
Liquids A and B form ideal solution over the entire range of composition. At temperature T, equimolar
binary solution of liquids A and B has vapour pressure 45 Torr. At the same temperature, a new solution of A and B having mole fractions xA and xB, respectively, has vapour pressure of 22.5 Torr. The value of xA/xB in the new solution is ____.
(given that the vapour pressure of pure liquid A is 20 Torr at temperature T)
|
3 videos|3 docs|40 tests
|
|
3 videos|3 docs|40 tests
|


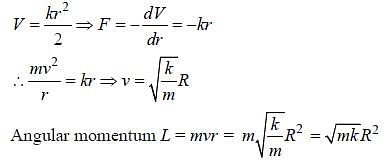
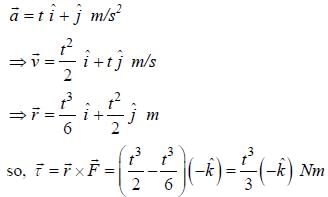
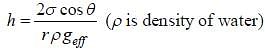
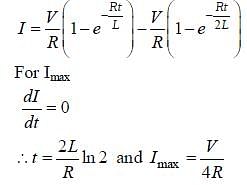
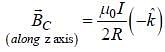
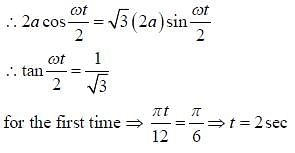
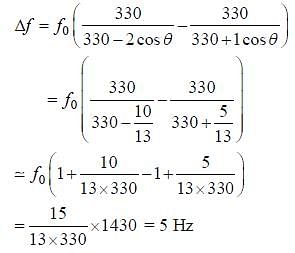
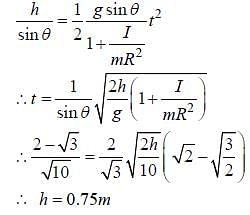
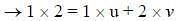
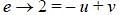
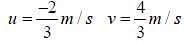
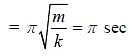
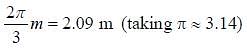
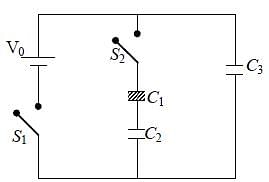
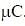 . when S1 opened and S2 closed, C3 has charge 5
. when S1 opened and S2 closed, C3 has charge 5 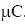 . so remaining 3
. so remaining 3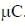 resides on C1 and C2
resides on C1 and C2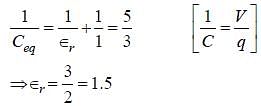
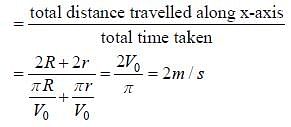
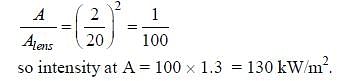
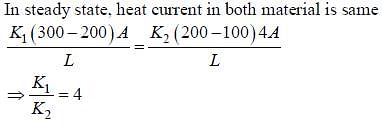

 ] and [
] and [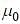 ] is
] is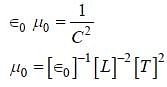

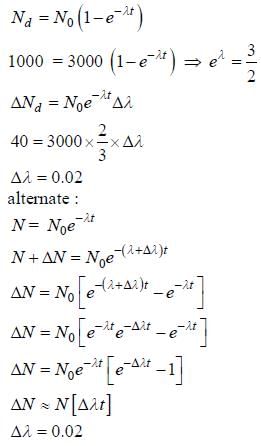
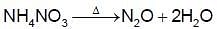 (N2O can further decompose to N2 and O2 at temperature above 300oC)
(N2O can further decompose to N2 and O2 at temperature above 300oC)