JEE Advanced 2013 Paper -1 with Solutions - JEE MCQ
30 Questions MCQ Test National Level Test Series for JEE Advanced 2025 - JEE Advanced 2013 Paper -1 with Solutions
SECTION – 1: (Only one option correct Type)
This section contains 10 multiple choice questions. Each question has four choice (A), (B), (C) and (D) out of which ONLY ONE is correct.
Q. 1 - 10 carry 2 marks each.
Q.
One end of a horizontal thick copper wire of length 2L and radius 2R is welded to an end of another
horizontal thin copper wire of length L and radius R. When the arrangement is stretched by applying forces
at two ends, the ratio of the elongation in the thin wire to that in the thick wire is
horizontal thin copper wire of length L and radius R. When the arrangement is stretched by applying forces
at two ends, the ratio of the elongation in the thin wire to that in the thick wire is
The work done on a particle of mass m by a force 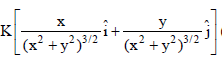 (K being a constant of appropriate dimensions, when the particle is taken from the point (a, 0) to the point (0, a) along a circular
(K being a constant of appropriate dimensions, when the particle is taken from the point (a, 0) to the point (0, a) along a circular
path of radius a about the origin in the x-y plane is
path of radius a about the origin in the x-y plane is
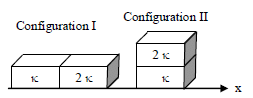
Two rectangular blocks, having identical dimensions, can be arranged either in configuration I or in configuration II as shown in the figure. One of the blocks has thermal conductivity k and the other 2k . The temperature difference between the ends along the x-axis is the same in both the configurations. It takes 9 s to transport a certain amount of heat from the hot end to the cold end in the configuration I. The time to transport the same amount of heat in the configuration II is
A ray of light travelling in the direction is incident on a plane mirror. After reflection, it travels
along the direction The angle of incidence is
The diameter of a cylinder is measured using a Vernier callipers with no zero error. It is found that the zero
of the Vernier scale lies between 5.10 cm and 5.15 cm of the main scale. The Vernier scale has 50 divisions
equivalent to 2.45 cm. The 24th division of the Vernier scale exactly coincides with one of the main scale
divisions. The diameter of the cylinder is
Two non-reactive monoatomic ideal gases have their atomic masses in the ratio 2 : 3. The ratio of their
partial pressures, when enclosed in a vessel kept at a constant temperature, is 4 : 3. The ratio of their
densities is
In the Young’s double slit experiment using a monochromatic light of wavelength λ, the path difference (in
terms of an integer n) corresponding to any point having half the peak intensity is
The image of an object, formed by a plano-convex lens at a distance of 8 m behind the lens, is real and is
one-third the size of the object. The wavelength of light inside the lens is 2/3 times the wavelength in free
space. The radius of the curved surface of the lens is
A particle of mass m is projected from the ground with an initial speed u0 at an angle α with the horizontal.
At the highest point of its trajectory, it makes a completely inelastic collision with another identical
particle, which was thrown vertically upward from the ground with the same initial speed u0. The angle that
the composite system makes with the horizontal immediately after the collision is
A pulse of light of duration 100 ns is absorbed completely by a small object initially at rest. Power of the
pulse is 30 mW and the speed of light is 3 x 108 m/s. The final momentum of the object is
SECTION – 2 : (One or more options correct Type)
This section contains 5 multiple choice questions. Each question has four choices (A), (B), (C) and (D) out of which ONE or MORE are correct.
Q. No. 11 -15 carry 4 marks each and 1 mark is deducted for incorrect answer
Q.
In the circuit shown in the figure, there are two parallel plate capacitors each of capacitance C. The switch
S1 is pressed first to fully charge the capacitor C1 and then released. The switch S2 is then pressed to charge
the capacitor C2. After some time, S2 is released and then S3 is pressed. After some time,
A particle of mass M and positive charge Q, moving with a constant velocity enters a region
of uniform static magnetic field normal to the x-y plane. The region of the magnetic field extends from x =
0 to x = L for all values of y. After passing through this region, the particle emerges on the other side after
10 milliseconds with a velocity The correct statement(s) is (are)
A horizontal stretched string fixed at two ends, is vibrating in its fifth harmonic according to the equation y(x, t) = 0.01m sin [(62.8m-1)x] cos[(628s-1)t]. Assuming π = 3.14, the correct statement(s) is (are)
A solid sphere of radius R and density ρ is attached to one end of a mass-less spring of force constant k.
The other end of the spring is connected to another solid sphere of radius R and density 3ρ. The complete
arrangement is placed in a liquid of density 2ρ and is allowed to reach equilibrium. The correct
statement(s) is (are)
Two non-conducting solid spheres of radii R and 2R, having uniform volume charge densities ρ1 and ρ2
respectively, touch each other. The net electric field at a distance 2R from the centre of the smaller sphere,
along the line joining the centre of the spheres is zero. The ratio ρ1/ρ2 can be
SECTION – 3 : (Integer value correct Type)
This section contains 5 questions. The answer to each question is a single digit integer, ranging from 0 to 9 (both inclusive).
Q. No. 16-20 carry 4 marks each and 1 mark is deducted for every incorrect answer
Q.
A bob of mass m , suspended by a string of length l1 is given a minimum velocity required to complete a
full circle in the vertical plane. At the highest point, it collides elastically with another bob of mass m
suspended by a string of length l2, which is initially at rest. Both the strings are mass-less and inextensible.
If the second bob, after collision acquires the minimum speed required to complete a full circle in the
vertical plane, the ratio l1/l2 is
A particle of mass 0.2 kg is moving in one dimension under a force that delivers a constant power 0.5 W to
the particle. If the initial speed (in m/s) of the particle is zero, the speed (in m/s) after 5 s is
The work functions of Silver and Sodium are 4.6 and 2.3 eV, respectively. The ratio of the slope of the
stopping potential versus frequency plot for Silver to that of Sodium is
A freshly prepared sample of a radioisotope of half-life 1386 s has activity 103 disintegrations per second.
Given that ln 2 = 0.693, the fraction of the initial number of nuclei (expressed in nearest integer percentage)
that will decay in the first 80 s after preparation of the sample is
A uniform circular disc of mass 50 kg and radius 0.4 m is rotating with an angular velocity of 10 rad s-1
about its own axis, which is vertical. Two uniform circular rings, each of mass 6.25 kg and radius 0.2 m,
are gently placed symmetrically on the disc in such a manner that they are touching each other along the
axis of the disc and are horizontal. Assume that the friction is large enough such that the rings are at rest
relative to the disc and the system rotates about the original axis. The new angular velocity (in rad s-1) of
the system is
SECTION – 1
Q. No. 21- 40 carry 2 marks each
This section contains 10 multiple choice questions. Each question has four choices (A), (B), (C) and (D) out of which ONLY ONE is correct.
Q.
In the reaction,
P+Q →R+S
the time taken for 75% reaction of P is twice the time taken for 50% reaction of P. The concentration of Q
varies with reaction time as shown in the figure. The overall order of the reaction is
Consider the following complex ions, P, Q and R
The correct order of the complex ions, according to their spin–only magnetic moment values (in B.M.) is
The arrangement of X– ions around A+ ion in solid AX is given in the figure (not drawn to scale). If the
radius of X– is 250 pm, the radius of A+ is
Concentrated nitric acid, upon long standing, turns yellow–brown due to the formation of
The compound that does NOT liberate CO2, on treatment with aqueous sodium bicarbonate solution, is
Methylene blue, from its aqueous solution, is adsorbed on activated charcoal at 250C. For this process, the
correct statement is
KI in acetone, undergoes SN2 reaction with each of P, Q, R and S. The rates of the reaction vary as
The standard enthalpies of formation of CO2(g), H2O(l) and glucose(s) at 250C are –400 kJ/mol,
–300 kJ/mol and –1300 kJ/mol, respectively. The standard enthalpy of combustion per gram of glucose at
250C is
Upon treatment with ammoniacal H2S, the metal ion that precipitates as a sulfide is
|
3 videos|2 docs|40 tests
|
|
3 videos|2 docs|40 tests
|


















