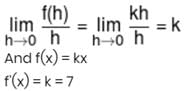JEE Main Maths Mock Test- 7 - JEE MCQ
25 Questions MCQ Test Mock Tests for JEE Main and Advanced 2025 - JEE Main Maths Mock Test- 7
In the following question, a Statement of Assertion (A) is given followed by a corresponding Reason (R) just below it. Read the Statements carefully and mark the correct answer-
Assertion(A) :A relation R on the set of complex number defined by Z1 R Z2 ⇔ Z1 − Z2 is real, is an equivalence relation.
Reason(R) :Reflexive and symmetric properties may not imply transitivity.
Assertion(A) :A relation R on the set of complex number defined by Z1 R Z2 ⇔ Z1 − Z2 is real, is an equivalence relation.
Reason(R) :Reflexive and symmetric properties may not imply transitivity.
The area contained between the curve x y = a2 , the vertical line x = a, x = 4a (a > 0) and x -axis is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Straight line px+qy+r=0 touches the circle x2+y2=a2 if
A circle passes through (0,0) and its centre lies on y=x. If it cuts the circle x2+y2-4x-6y+10=0 orthogonally, then its equation is
In the following question, a Statement of Assertion (A) is given followed by a corresponding Reason (R) just below it. Read the Statements carefully and mark the correct answer-
Let n ≥ 3 and let the complex numbers α1 , α2 , . . . , αn be the roots of xn − 1 = 0 with α1 = 1 .
Assertion(A) :For any positive integer is again a positive integer.
Reason(R) :For any positive integer
If y=x2(x-2)2, then the values of x for which y is increasing, are
Let the function f be defined by f(x) = 2x + 1/1- 3x. Then f⁻1(x) is
In the following question, a Statement of Assertion (A) is given followed by a corresponding Reason (R) just below it. Read the Statements carefully and mark the correct answer-
Assertion(A): If f : R → R defined by f (x) = x3 then f is one one onto
Reason(R) : Function f is strictly decreasing on R.
In the following question, a Statement of Assertion (A) is given followed by a corresponding Reason (R) just below it. Read the Statements carefully and mark the correct answer-
Assertion(A): y = sin (ax + b) is a general solution of y" + a2 y = 0 .
Reason(R) : y = sin (ax + b) is a trigonometric function.
If A is a square matrix such that A2 = I, then A⁻1 is equal to
If x+y+1=0 tocuhes the parabola y2=λx,then λ is equal to
A polygon has 44 diagonals. The number of its sides is
If P(B)=(3/4), P(A∩B∩C̅) = (1/3) and P(A̅∩B∩C̅) = 1/3, then P(B∩C) is
Given n = 10, ∑x = 4, ∑y = 3, ∑x2 = 8, ∑y2 = 9 and ∑xy = 3, then coefficient of correlation is
The straight line x + y = a will be a tangent to the ellipse x2/9 + y2/16 = 1 if a =
Let f(x) = [2x3 – 5]; then number of points in (1, 2) where the function is discontinuous are where [.] → G.I.F.
Let f(x) be a function given by
f(x + y) = f(x) + f(y) for all x, y. Let f '(5) exist and is equal to 7, then 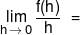 ?
?
The equation of the perpendicular bisectors of the sides AB and AC of a triangle ABC are y = x and y = –x, respectively. If the point A is (1, 2), then the area of ΔABC is :-
If the foci of the ellipse 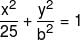 and the hyperbola
and the hyperbola 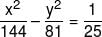 coincide, then the value of b2 is:-
coincide, then the value of b2 is:-
|
357 docs|148 tests
|
|
357 docs|148 tests
|


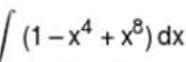
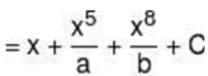 then the value of a + b is:
then the value of a + b is: