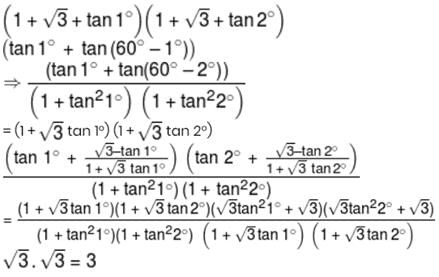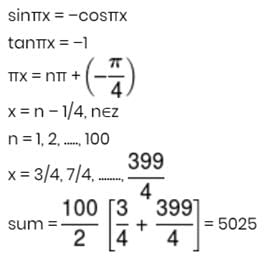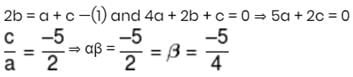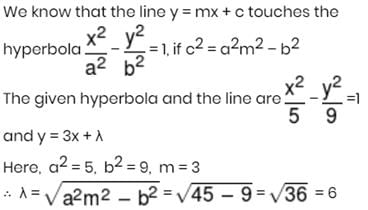JEE Exam > JEE Tests > Mock Tests for JEE Main and Advanced 2025 > JEE Main Maths Test- 2 - JEE MCQ
JEE Main Maths Test- 2 - JEE MCQ
Test Description
25 Questions MCQ Test Mock Tests for JEE Main and Advanced 2025 - JEE Main Maths Test- 2
JEE Main Maths Test- 2 for JEE 2024 is part of Mock Tests for JEE Main and Advanced 2025 preparation. The JEE Main Maths Test- 2 questions and answers have been
prepared according to the JEE exam syllabus.The JEE Main Maths Test- 2 MCQs are made for JEE 2024 Exam. Find important
definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for JEE Main Maths Test- 2 below.
Solutions of JEE Main Maths Test- 2 questions in English are available as part of our Mock Tests for JEE Main and Advanced 2025 for JEE & JEE Main Maths Test- 2 solutions in
Hindi for Mock Tests for JEE Main and Advanced 2025 course. Download more important topics, notes, lectures and mock
test series for JEE Exam by signing up for free. Attempt JEE Main Maths Test- 2 | 25 questions in 60 minutes | Mock test for JEE preparation | Free important questions MCQ to study Mock Tests for JEE Main and Advanced 2025 for JEE Exam | Download free PDF with solutions
JEE Main Maths Test- 2 - Question 1
Mid-points of the sides AB and AC of a 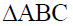 are (3,5) and (–3,–3) respectively, then the length of the side BC is
are (3,5) and (–3,–3) respectively, then the length of the side BC is
Detailed Solution for JEE Main Maths Test- 2 - Question 1
JEE Main Maths Test- 2 - Question 2
The co-ordinates of the middle points of the sides of a triangle are (4,2),(3,3) and (2,2), then the coordinates of its centroid are
Detailed Solution for JEE Main Maths Test- 2 - Question 2
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
JEE Main Maths Test- 2 - Question 3
If a and b are real numbers between 0 and 1 such that the points (a,1),(1,b) and (0,0) form an equilateral triangle, then a, b are
Detailed Solution for JEE Main Maths Test- 2 - Question 3
Detailed Solution for JEE Main Maths Test- 2 - Question 4
JEE Main Maths Test- 2 - Question 5
The straight lines joining the origin to the points of intersection of the line 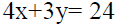 with the circle
with the circle 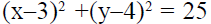 are
are
Detailed Solution for JEE Main Maths Test- 2 - Question 5
JEE Main Maths Test- 2 - Question 6
The area of circle centred at (1,2) and passing through (4,6) is
Detailed Solution for JEE Main Maths Test- 2 - Question 6
Detailed Solution for JEE Main Maths Test- 2 - Question 7
JEE Main Maths Test- 2 - Question 8
A diameter of 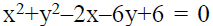 is a chord to circle centre (2,1), then radius of the circle is
is a chord to circle centre (2,1), then radius of the circle is
Detailed Solution for JEE Main Maths Test- 2 - Question 8
JEE Main Maths Test- 2 - Question 9
In the parabola 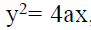 , the length of the chord passing through the vertex and inclined to the axis at an angle
, the length of the chord passing through the vertex and inclined to the axis at an angle 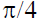 is
is
Detailed Solution for JEE Main Maths Test- 2 - Question 9
JEE Main Maths Test- 2 - Question 10
The angle made by a double ordinate of length 8a at the vertex of the parabola 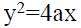 is
is
Detailed Solution for JEE Main Maths Test- 2 - Question 10
Detailed Solution for JEE Main Maths Test- 2 - Question 11
JEE Main Maths Test- 2 - Question 12
The line y = mx + 1 is a tangent to the parabola y2 = 4ax, if
Detailed Solution for JEE Main Maths Test- 2 - Question 12
Detailed Solution for JEE Main Maths Test- 2 - Question 13
JEE Main Maths Test- 2 - Question 14
An ellipse has OB as a semi minor axis. F,F` are its foci, and the angle FBF` is a right angle. Then the eccentricity of the ellipse is
Detailed Solution for JEE Main Maths Test- 2 - Question 14
JEE Main Maths Test- 2 - Question 15
If the straight line is a tangent to the ellipse
, then c will be equal to
Detailed Solution for JEE Main Maths Test- 2 - Question 15
JEE Main Maths Test- 2 - Question 16
The eccentricity of the hyperbola with latus rectum 12 and semi-conjugate axis 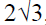 , is
, is
Detailed Solution for JEE Main Maths Test- 2 - Question 16
JEE Main Maths Test- 2 - Question 17
If 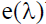 be the eccentricity of rectangular hyperbola
be the eccentricity of rectangular hyperbola 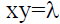 then the value of e(1)–e(6) is
then the value of e(1)–e(6) is
Detailed Solution for JEE Main Maths Test- 2 - Question 17
JEE Main Maths Test- 2 - Question 18
If e and e` be the eccentricities of two conics S and S` such that 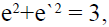 then both S and S` are
then both S and S` are
Detailed Solution for JEE Main Maths Test- 2 - Question 18
Detailed Solution for JEE Main Maths Test- 2 - Question 19
Detailed Solution for JEE Main Maths Test- 2 - Question 20
*Answer can only contain numeric values
Detailed Solution for JEE Main Maths Test- 2 - Question 21
*Answer can only contain numeric values
JEE Main Maths Test- 2 - Question 22
Find number of surjection from A to B where
A= {1, 2, 3, 4}, B = {a, b}:
*Answer can only contain numeric values
JEE Main Maths Test- 2 - Question 23
Sum of all the solution of equation sinπx + cosπx= 0 in x ∈ [0, 100]
Detailed Solution for JEE Main Maths Test- 2 - Question 23
*Answer can only contain numeric values
JEE Main Maths Test- 2 - Question 24
If a,b,c are in A.P. and one root of ax2 + bx + c = 0 is 2 then other root is?
Detailed Solution for JEE Main Maths Test- 2 - Question 24
*Answer can only contain numeric values
JEE Main Maths Test- 2 - Question 25
If the line y = 3x + λ touches the hyperbola 9x2 – 5y2 = 45, then the value of λ is
Detailed Solution for JEE Main Maths Test- 2 - Question 25
|
357 docs|148 tests
|
Information about JEE Main Maths Test- 2 Page
In this test you can find the Exam questions for JEE Main Maths Test- 2 solved & explained in the simplest way possible.
Besides giving Questions and answers for JEE Main Maths Test- 2, EduRev gives you an ample number of Online tests for practice
|
357 docs|148 tests
|
Download as PDF



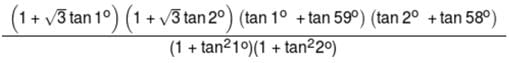 is:-
is:-