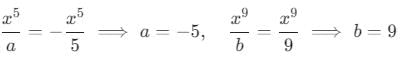JEE Main Part Test - 1 - JEE MCQ
30 Questions MCQ Test - JEE Main Part Test - 1
The length, breadth and thickness of a rectangular sheet of metal are 4.234 m, 1.005 m, and 2.01 cm respectively. Give the volume of the sheet to correct significant figures.
Population of a town is reported as 157,900 (rounded to the nearest hundred). Which of the following statements is correct?
The range R of projectile is same when its maximum height are h1 and h2. What is the relation between R, h1 and h2?
A wheel is subjected to uniform angular acceleration about its axis. Initially its angular velocity is zero. In the first 2 sec, it rotates through an angle q1; in the next 2 sec it rotates through an additional angle θ2, the ratio θ2/θ1 is
Two cars are moving in same direction with speed of 30 kmph. They are separated by a distance of 5 km. What is the speed of a car moving in opposite direction if it meets the two cars at an interval of 4 min?
A body starts from rest, the ratio of distances travelled by the body during 3rd and 4thseconds is :
Adjoining figure shows a force of 40 N acting at 30° to the horizontal on a body of mass 5 kg resting on a smooth horizontal surface. Assuming that the acceleration of free-fall is 10 ms_2, which of the following statements A, B, C is (are) correct?
[1] The horizontal force acting on the body is 20 N
[2] The weight of the 5 kg mass acts vertically downwards
[3] The net vertical force acting on the body is 30 N
A ring of mass 200 gram is attached to one end of a light spring of force constant 100 N/m and natural length 10 cm. The ring is constrained to move on a rough wire in the shape of the quarter ellipse of the major axis 24 cm and the minor axis 16 cm with its centre at the origin. The plane of the ellipse is vertical and wire is fixed at points A and B as shown in the figure. Initially, ring is at A with other end of the spring fixed at the origin. If normal reaction of wire on ring at A is zero and ring is given a horizontal velocity of 10 m/s towards right so that it just reaches point B, then select the correct alternative (s) (g = 10 m/s2)
Which of the following options are correct,
where i, j and k are unit vectors along the x, y and z axis?
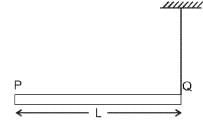
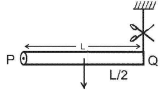
A rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in the figure. When the string is cut, the initial angular acceleration of the rod is:
[2013]
Electromagnetic radiations having λ = 310 Å are subjected to a metal sheet having work function = 12.8 eV. What will be the velocity of photoelectrons with maximum Kinetic energy.
Consider the ground state of Cr atom (X = 24). The number of electrons with the azimuthal quantum numbers, ℓ = 1 and 2 are, respectively [2004]
Which of the following sets of quantum numbers is correct for an electron in 4f orbital ? [2004]
Radial probability density in the occupied orbital of a hydrogen atom in the ground state (1s) is given below
In the general electronic configuration -
(n - 2)f1-14 (n - 1)d0-1 ns2, if value of n = 7 the configuration will be -
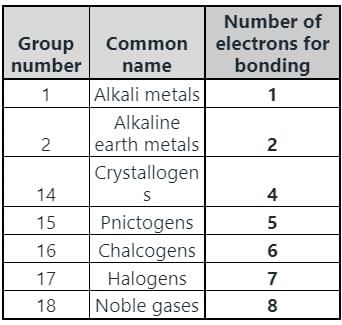
In which group of the modern periodic table are halogens placed?
The symbol for element with atomic number 111 and name Unununium is
Which of the following angle corresponds to sp2 hybridisation?
The domain of the function √(log1/3 log4 ([x]2 - 5)) is (where [x] denotes greatest integer function)
A real valued function f(x) satisfies the functional equation f(x – y) = f(x) f(y) – f(a – x) f(a + y) where a is a given constant and f(0) = 1, f(2a – x) is equal to
If z ≠ 1 and 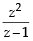 is real, then the point represented by the complex number z lies : [2012]
is real, then the point represented by the complex number z lies : [2012]
If the function ƒ(x) = 2 + x2 – e–x and g(x) = ƒ–1(x), then the value of 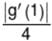 equals
equals
If function ƒ(x) = x3 + ax2 + bx + c is monotonically increasing ∀ x ∈ R, where a & b are prime numbers less than 10, then number of possible ordered pairs (a,b) is



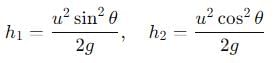
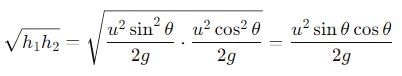
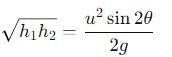
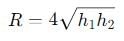
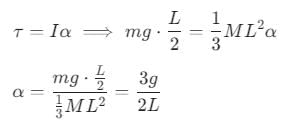
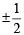
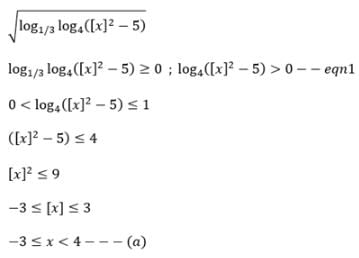

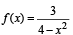
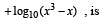
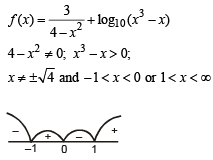
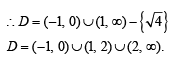
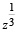 = p+ iq, then
= p+ iq, then 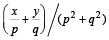 is equal to [2004]
is equal to [2004]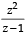 is real ⇒ Im
is real ⇒ Im 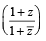 = 0
= 0
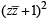
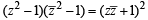

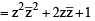
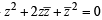 ⇒
⇒ 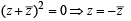
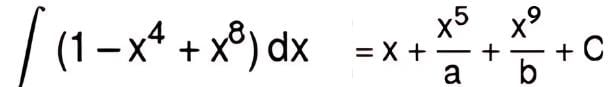 then the value of a + b is:
then the value of a + b is: 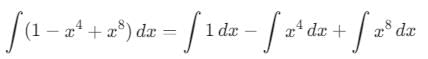
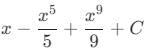
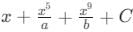 :
: