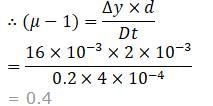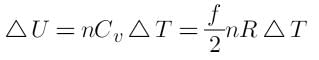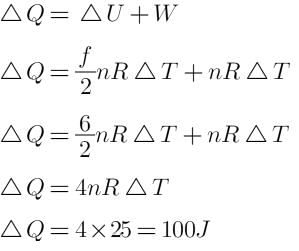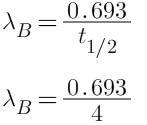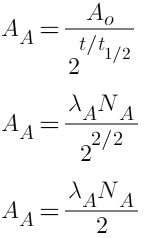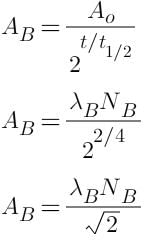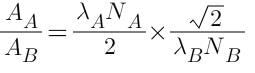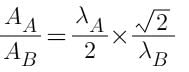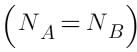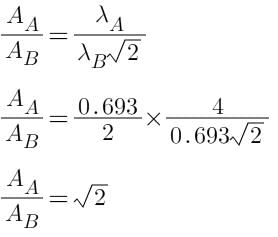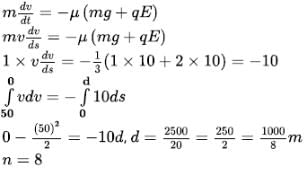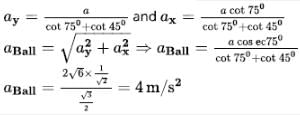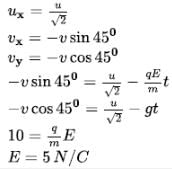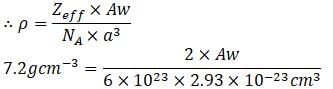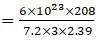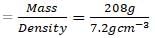JEE Main Practice Test- 5 - JEE MCQ
30 Questions MCQ Test Mock Tests for JEE Main and Advanced 2025 - JEE Main Practice Test- 5
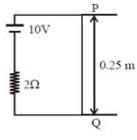
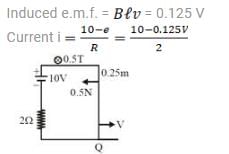
A metal wire PQ slides on parallel metallic rails having separation 0.25 m, each having negligible resistance. There is a 2Ω resistor and 10V battery as shown in figure. There is a uniform magnetic field directed into the plane of the paper of magnitude 0.5 T. A force of 0.5N to the left is required to keep the wire PQ moving with constant speed to the right. With what speed is the wire PQ moving? (Neglect self-inductance of the loop)

In the given figure a ring of mass m is kept on a horizontal surface while a body of equal mass 'm' attached through a string, which is wounded on the ring. When the system is released the ring rolls without slipping. Consider the following statements and choose the correct option.
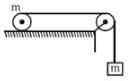
(i) acceleration of the centre of mass of ring is g/3
(ii) acceleration of the hanging particle is 2g/3
(iii) frictional force (on the ring) acts along forward direction
(iv) frictional force (on the ring) acts along backward direction

(i) acceleration of the centre of mass of ring is g/3
(ii) acceleration of the hanging particle is 2g/3
(iii) frictional force (on the ring) acts along forward direction
(iv) frictional force (on the ring) acts along backward direction
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
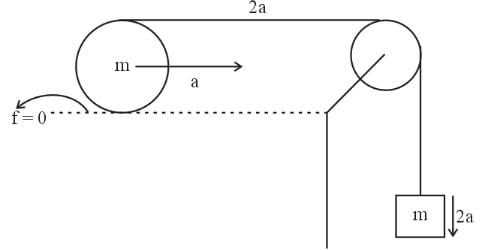
A concave mirror gives a real image magnified 6 times when the object is moved 6 cm the magnification of the real image is 4 times. What will be the focal length of the mirror?
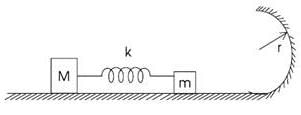
A spring mass system with unequal masses is placed at rest on a smooth horizontal surface. The spring is initially kept compressed with a thread. When the spring is cut, the mass m moves so as to enter in a vertical circular loop of radius r. The minimum compression x in the spring so that the mass m may negotiate the vertical loop is
A plane electromagnetic wave of angular frequency ω propagates in a poorly conducting medium of conductivity σ and relative permittivity ε. Find the ratio of conduction current density and displacement current density in the medium.
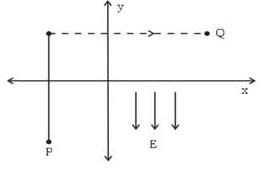
A uniform electric field of magnitude 245 V/m is directed in the negative y direction as shown in figure. The coordinates of point P and Q are (- 0.5m, - 0.8m) and (0.3m, 0.7m) respectively. Calculate the potential difference VQ - VP along the path shown in the figure,
A cylinder of radius r = 1 m and height 3 m filled with a liquid upto 2 m high and is rotated about its vertical axis as shown in the Figure.
The speed of rotation of the cylinder when the point at the centre of the base is just exposed is

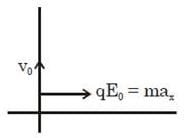
A charge particle q of mass m0 is projected along the y-axis at t = 0 from origin with a velocity V0. If a uniform electric field E0 also exists along the x-axis, then the time at which the de-Broglie wavelength of the particle becomes half of the initial value is:
The beat frequency produced when the following two waves x1 = 12 sin (484πt − 7πx) and x2 = 12 sin (480πt − 7πx) are sounded together is
An 80 kg man standing on ice throws a 4 kg body horizontally at 6 ms−1. The frictional coefficient between the ice and his feet is 0.02. The distance through which the man slips is (g = 10 ms−2)
Liquid cools from 50ºC to 45 ºC in 5 minutes and from 45ºC to 41.5ºC in the next 5 minutes. The temperature of the surrounding is :- [Assume newton's law of cooling is applicable]
A long solenoid of self-inductance L and area of cross section A not carrying any current is placed in a uniform magnetic field of strength B with its axis parallel to the field direction. The total magnetic flux linked with the solenoid is φ. The energy of the magnetic field stored in the solenoid is
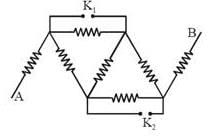
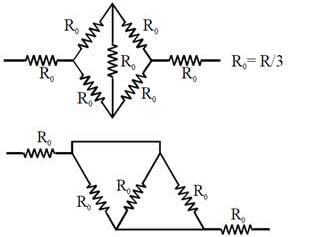
All wires have same resistance and equivalent resistance between A and B is R. Now keys are closed, then the equivalent resistance will become:-
Steam at 100°C is passed into 1.4 kg of water kept in a calorimeter of water equivalent 0.03 kg at 20 °C till the temperature of the calorimeter and contents reach 80°C. Latent heat of steam is 2.26 × 106 J kg − 1 and sp.heat capacity of water is 4200 J /kg/°C. The mass of steam condensed in kilogram is nearly equal to
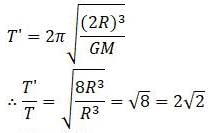
A satellite orbiting around the earth of radius R is shifted to an orbit of radius 2R. The time taken for one revolution will increase nearly by
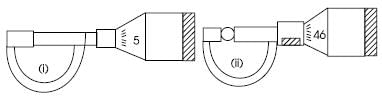
Screw gauge shown in Figure has 50 divisions and in one complete rotation of circular scale the main scale moves 0.5 mm.
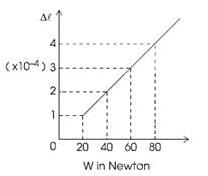
The given graph shows the extension (Δl) of a wire of length 1.0 m suspended from the top of a roof at one end and loaded at the other end. If the cross sectional area of the wire is 10− 6m2, the Young’s modulus Y of the material of the wire is
In Young’s double slit experiment, a monochromatic light of wavelength 5500 Å is used. The slits are 2 mm apart. The fringes are formed on a screen placed 20 cm away from the slits. It is found that the interference pattern shifts by 16 mm when a transparent plate of thickness 0.4 mm is introduced in the path of one of the slits. The refractive index of the transparent plate is
The average degree of freedom per molecule of a gas is 6. The gas performs 25 J work, while expanding at constant pressure. The heat absorbed by the gas is:-
The radioactive sources A and B have half lives of 2hr and 4hr respectively, initially contain the same number of radioactive atoms. At the end of 2 hours, their rates of distintegration are in the ratio:-
A Young's double slit apparatus is immersed in a liquid of refractive index 1.33. It has slit separation of 1 mm and interference pattern is observed on the screen at a distance 1.33 m from plane of slits. The wavelength of light used in air is 6300A°. When one of the slit is covered by a glass sheet of thickness 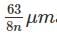 and refractive index 1.53, the position of maxima and minima get interchanged. Find the maximum possible value of n.
and refractive index 1.53, the position of maxima and minima get interchanged. Find the maximum possible value of n.
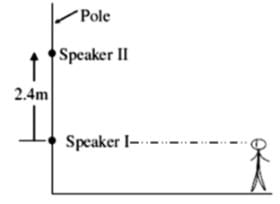
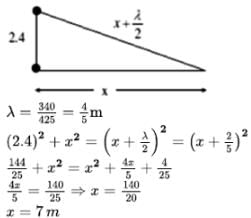
An oscillator of frequency 425 Hz drives two speakers. The speaker are fixed on a vertical pole at a distance 2.4m from each other. A person whose height (of ears) is same as that of lower speaker runs horizontally away from the two speakers. Find the maximum distance (in m) of person from the pole where he hears no sound, (velocity of sound in air 340 m/s)
A particle of mass m = 1 kg and having charge Q = 2C is projected on a rough horizontal xy plane from (4, 0, 0) m with velocity 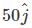 and in the region there exist a uniform electric field
and in the region there exist a uniform electric field 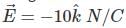 and a uniform magnetic field
and a uniform magnetic field 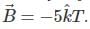 The coefficient of friction between the particle and the horizontal surface is μ = 1/3 and the particle comes to rest by moving a distance 1000/n metres. Find n.
The coefficient of friction between the particle and the horizontal surface is μ = 1/3 and the particle comes to rest by moving a distance 1000/n metres. Find n.
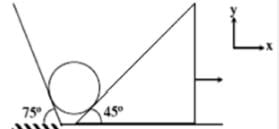
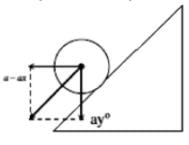
A wedge of inclination 45° is moved towards right with a constant acceleration of 2√6 m/s2 as shown in figure. Find magnitude of acceleration of the ball placed between an inclined wall and the wedge.
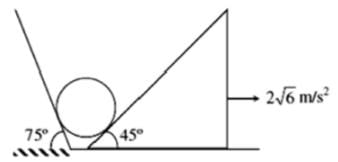
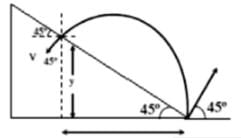
In the situation shown in figure, a particle having charge q = 2C and mass = 1 kg is projected from bottom of an inclined plane of inclination 45° at an angle 45° with horizontal, so that the particle strike the inclined plane normally due to a uniform horizontal electric field E. Find the value of E (in NC-1)
Ratio of Boyle temperature and critical temperature of gas is:
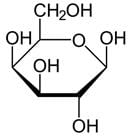
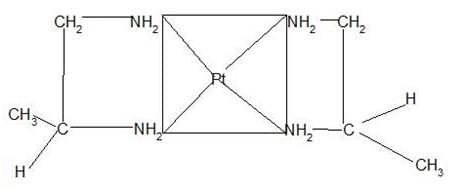
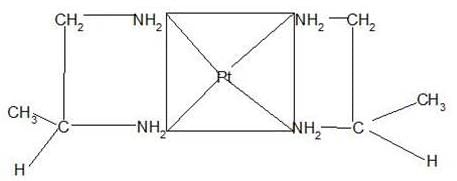
Which of the following complex square having planner complex can exhibit geometrical isomerism?
An element has a bcc structure with a cell edge of 288 pm. The density of the element is 7.2 g cm–3. Number of atoms present in 208 g of the element ?
The most acidic oxyacid of halogen among the given option is
|
357 docs|148 tests
|
|
357 docs|148 tests
|



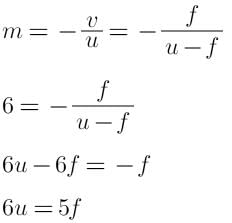
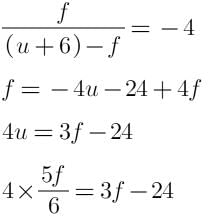
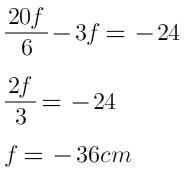
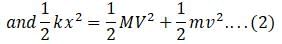
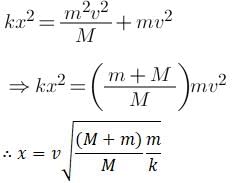
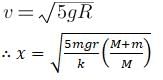
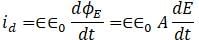
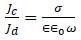
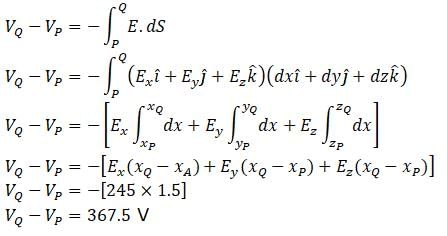
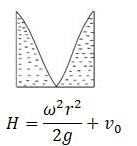
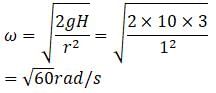
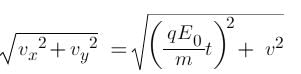
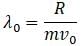

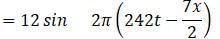
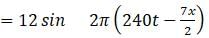

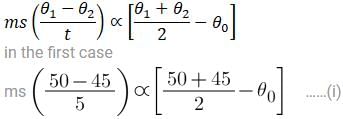
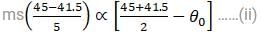
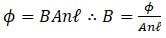
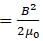
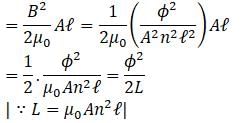
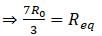
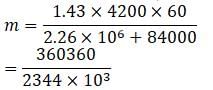
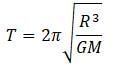
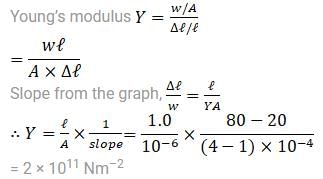
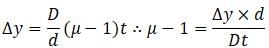 Δy = 16 mm = 16 × 10− 3 m
Δy = 16 mm = 16 × 10− 3 m