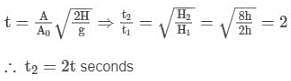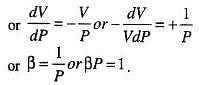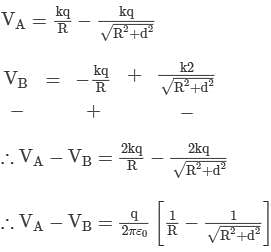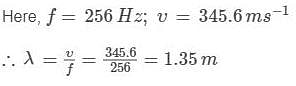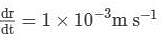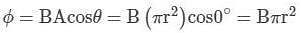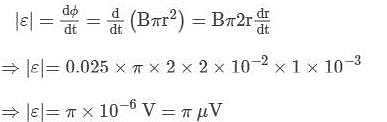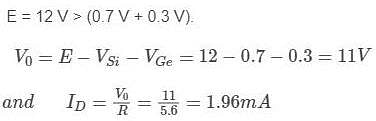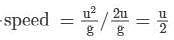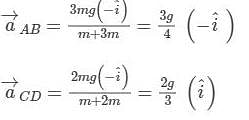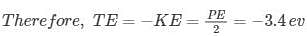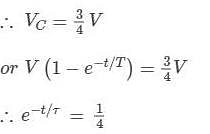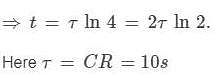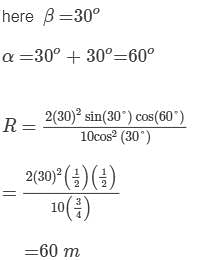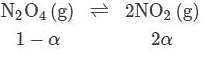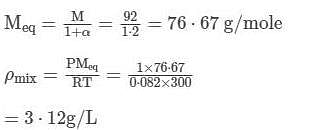JEE Main Practice Test- 6 - JEE MCQ
30 Questions MCQ Test Mock Tests for JEE Main and Advanced 2025 - JEE Main Practice Test- 6
Water is filled up to a height 'h' in a cylindrical vessel. Now, a hole of area 'A' is made at bottom of the vessel. Water drains out of the hole in time 't' seconds. If we repeat the above process with a height of water as '4h', then how much time it require for water to drain out of the cylinder?
[Assume A << A0 (area of tank)]
[Assume A << A0 (area of tank)]
Which of the following graphs correctly represent the variation of β = −[(dV/dp)/V] with p for an ideal gas at constant temperature?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
What is the potential difference between A and B?
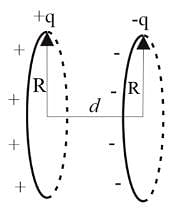
(where A is the centre of left ring and B is the centre of right ring)

Half-life of a radioactive substance A is 4 days. The probability of a nucleus that, from the given sample that it will decay in two half-lives is
Which of the following statement is false for electromagnetic waves ?
The voltage of clouds is 4 × 106 V with respect to ground. In a lightning strike lasting 100 ms, a charge of 4 C is delivered to the ground. The average power of lightning strike is (assume complete discharges)
A tuning fork vibrates with a frequency of 256 Hz. Taking the speed of sound to be 345.6 m s-1 in the air, find the wavelength and the distance, which the sound travels during the time, fork makes 60 vibrations.
If the radius of the earth were to shrink by one percent and its mass remains the same, the acceleration due to gravity on the earth's surface would
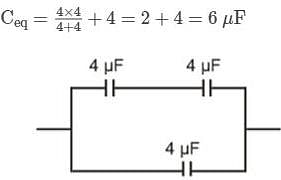
Three capacitors each of capacity 4 μF are to be connected in such a way that the effective capacitance is 6 μF. This can be done by
Six wires of current I1 = 1A, I2 = 2A, I3 = 3A, I4 = 1A, I5 = 5A and I6 = 4A cut the page perpendicularly at the points 1,2,3,4,5 and 6 respectively as shown in the figure. Find the value of integral ∮B→.dℓ around the circular path c.

A conducting circular loop is placed in a uniform magnetic field, B = 0.025 T with its plane perpendicular to the direction of magnetic field. The radius of the loop is made to shrink at a constant rate of 1 mm s-1. Find the induced emf in the loop when it's radius is 2 cm.
A body executing S.H.M. has amplitude 5 cm and frequency 5 vibrations per second. Calculate the displacement of particle from mean position after 0.32 s.
For network shown in figure, determine V0 and ID. (Where, ID = Current flowing in the diodes)

A particle is projected vertically upwards with a velocity u, from a point O. When it returns to the point of projection, which of the following is incorrect ?
Two blocks each of mass m, lie on a smooth table. They are attached to two other masses as shown in figure. The pulleys and strings are light. An object O is kept at rest on the table. The sides AB and CD of the two blocks are made reflecting. The acceleration of two images formed in those two reflecting surfaces with respect to each other is

An electron is in an excited state in a hydrogen like atom. It has a total energy of -3.4 eV. The kinetic energy is E and its de Broglie wavelength is λλ. Then
Two cylindrical rods of uniform cross-sectional area A and 2A, having free electrons per unit volume 2n and n respectively are joined in series. A constant current I flows through them in steady state. The ratio of drift velocity of free electrons in the left rod to that of the right rod is (VL/VR) is:

Uncharged capacitor of capacitance 4 μF4 and a resistance of 2.5 M ΩM Ω are connected in series with 12 V battery at t=0. Find the time after which the potential difference across the capacitor is 3 times the potential difference across the resistor. [Given, ln (2) = 0.693]
A refrigerator is to maintain the eatables, kept inside it, at 9oC. The coefficient of performance of the refrigerator, if the room temperature is 36oC, is
A ball is projected up an incline of 30o with a velocity of 30 ms−1 at an angle of 30o with reference to the inclined plane from the bottom of the inclined plane. If g = 10 ms−2, then the range on the inclined plane is
Three balls A, B and C whose masses are m, km and 4m respectively kept at rest on the horizontal smooth surface, as shown in the figure. The ball A is given velocity v0, rightward and it collides with the ball B elastically. Then ball B collides elastically third ball C. For what value of k, does the third ball C receive the maximum speed?

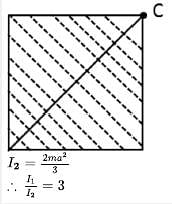
ABCDECA is a planar body of mass m of uniform thickness and same material. The dimensions are as shown in the figure. The moment of inertia of the body about an axis passing through point A and perpendicular to planar body is 11 and that of about an axis passing through C and perpendicular to planer body is l2. If 11/12 is k. Find the l value of k.
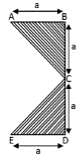
A body of mass 6.25 kg is travelling in a horizontal straight line with a velocity of 3 m/sec when a horizontal force P is applied to it at right angle to the initial direction of motion. If P varies according to the accompanying graph, remains constant in direction and is the only force acting on the body in its plane of motion, find the magnitude of the velocity of the body when t = 2 sec.

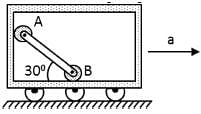
If a car is moving rightward with acceleration 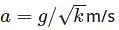 rightward as shown in the figure. Find the value of k so that, rod maintains its orientation as shown in the figure. Neglect the friction and mass of the small rollers at A and B.
rightward as shown in the figure. Find the value of k so that, rod maintains its orientation as shown in the figure. Neglect the friction and mass of the small rollers at A and B.
For identical rods, each of mass m are welded at their ends to form a square, and the corners are then welded to a light metal hoop of radius r. If the rigid assembly of rods and hoop is allowed to roll down the inclined rough surface. If the minimum value of the coefficient of static friction which will prevent slipping is k/10
Find the value of k.

If the nitrogen atom had electronic configuration 1s7, it would have energy lower than that of the normal ground state configuration 1s2 2s2 2p3, because the electrons would be closer to the nucleus, yet 1s7 is not observed because it violates
How many EDTA (ethylenediaminetetraacetic acid) molecules are required to make an octahedral complex with a Ca2+
The first orbital of H is represented by 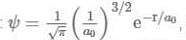 where a0 is Bohr's radius The probability of finding the electron at a distance r, from the nucleus in the region dV is
where a0 is Bohr's radius The probability of finding the electron at a distance r, from the nucleus in the region dV is
20% of N2O4 molecules are dissociated in a sample of gas at 27∘C and 760 torr. Mixture has the density at equilibrium equal to:
|
357 docs|148 tests
|
|
357 docs|148 tests
|