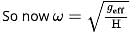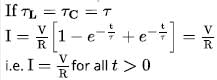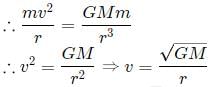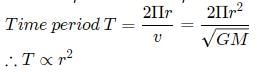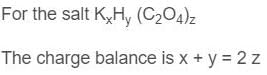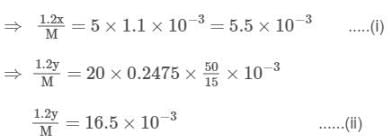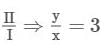JEE Main Practice Test- 8 - JEE MCQ
30 Questions MCQ Test Mock Tests for JEE Main and Advanced 2025 - JEE Main Practice Test- 8
In the figure shown the acceleration of A is, 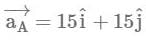 , then the acceleration of B is : (A remains in contact with B)
, then the acceleration of B is : (A remains in contact with B)
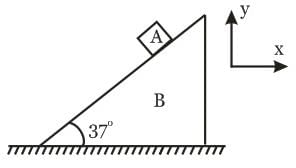
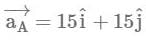 , then the acceleration of B is : (A remains in contact with B)
, then the acceleration of B is : (A remains in contact with B)
The speed of sound in hydrogen gas at N.T.P. is 1,328 ms-1. What will be its value in air at N.T.P., if density of hydrogen is 1/16th that of air?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A balloon that is initially flat, is inflated by filling it from a tank of compressed air. The final volume of the balloon is 5m3. The barometer reads 95 kPa. The work done in this process is
Two bodies of same mass tied with an inelastic string of length  together on a horizontal surface. One a horizontal surface of them is projected vertically upwards with velocity
together on a horizontal surface. One a horizontal surface of them is projected vertically upwards with velocity  Find the maximum height up to which the centre of mass of system of the two masses rises.
Find the maximum height up to which the centre of mass of system of the two masses rises.
The electric potential at a point (x, y, z) is given by V = -x2y - xz3 + 4 The electric field 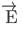 at that point is
at that point is
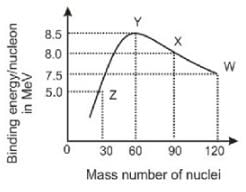
Binding energy per nucleon versus mass number curve for nuclei is shown in figure. W, X, Y and Z are four nuclei indicated on the curve. The process that would release energy is
A wire of length 1.0 m and radius 10-3 m is carrying a heavy current and is assumed to radiate as a black body. At equilibrium, its temperature is 900 K while that of the surroundings is 300 K. The resistivity of the material of the wire at 300 K is π2 × 10-8 ohm-m and its temperature coefficient of resistance is 7.8× 10−3 Co. Find the current in the wire. [Given Stefan's constant = 5.68 × 10-8 W/m2K4]
50 V battery is supplying a steady current of 10 amp when connected to an external resistor. If the efficiency of the battery at this current is 25%, then internal resistance of battery is:
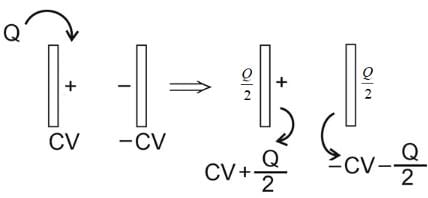
A capacitor of capacitance C is charged to a potential difference V from a cell and then disconnected from it. A charge +Q is now given to its positive plate. Now, the potential difference across the capacitor is.
Energy from the sun falls on the earth at a rate of 1353 W/m2, which is known as solar constant, i.e., the power incident per unit area per second at the top of atmosphere. Find the r.m.s values of the electric and magnetic fields in the sunlight reaching the top of the atmosphere.
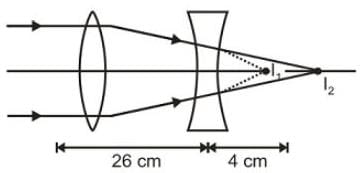
The size of the image of an object, which is at infinity, is formed by a convex lens of focal length 30 cm is 2 cm. If a concave lens of focal length 20 cm is placed between the convex lens and the image at a distance of 26 cm from the convex lens, calculate the new size of the image
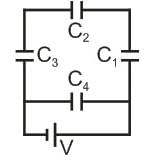
A network of Four capacitors of capacity equal to C1 = C, C2 = 2C, C3 = 3C and C4 = 4C, are connected to a battery as shown in the figure. The ratio of the charges on C2 and C4 is
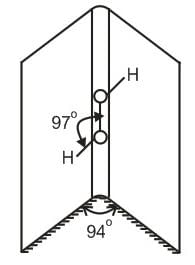
A rod AD, consisting of three segments AB, BC and CD joined together, is hanging vertically from a fixed support at A. The lengths of the segments are respectively 0.1 m, 0.2 m and 0.15 m. The cross - section of the rod is uniform 10-4 m2. A weight of 10 kg is hung from D. Calculate the displacements of point D if YAB = 2.5 x 1010 N/m2, YBC = 4 x 1010 N/m2 and YCD = 1 x 1010 N/m2. (Neglect the weight of the rod.)
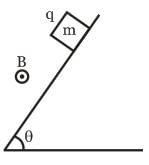
A block of mass m & charge q is released on a long smooth inclined plane. Magnetic field B is constant, uniform, horizontal and out of the plane of paper as shown. Find the time from start when block loses contact with the surface.
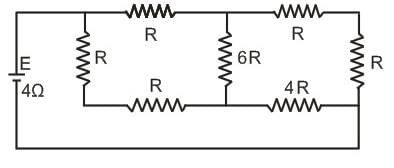
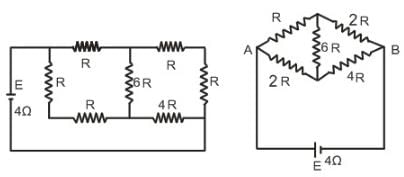
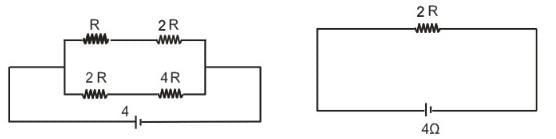
A battery of internal resistance 4Ω is connected to the network of resistances as shown in figure. In order that the maximum power can be delivered to the network, the value of R in $$ should be
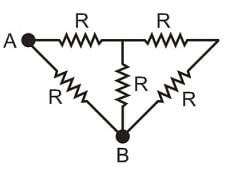
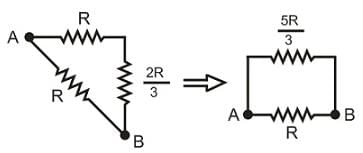
In the circuit shown in diagram, the equivalent resistance between point A and B is
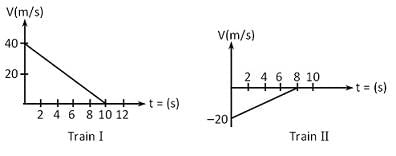
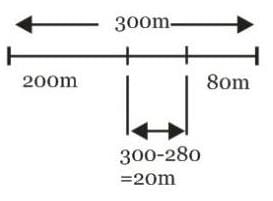
Two trains, which are moving along different tracks in opposite directions, are put on the same track due to a mistake. Their drivers, on noticing the mistake, start slowing down the trains when they are 300 m apart. Graphs given below show their velocities as a function of time as they slow down. The separation between the trains, when both have stopped, is:
A tuning fork sends out waves of wavelength 68.75 cm and 3 m in air and hydrogen gas respectively. If the velocity of sound in air is 330 ms-1, find the velocity of sound in hydrogen. Also, find the frequency of the tuning fork
A particle executes S.H.M. given by x = 0 · 24 cos (400 t - 0.5) in SI units. Find amplitude
A lens (μ = 1.5) is coated with a thin film of refractive index 1.2 in order to reduce the reflection from its surface at λ = 4800 Å. Find the minimum thickness of the film which will minimise the intensity of the reflected light. (Assume near normal incidence)
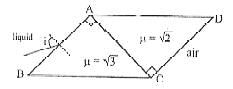
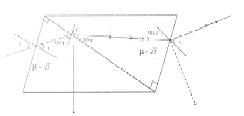
A ray of light from a liquid (μ = √3) is incident on a system of two right angled prism of refractive indices √3 and √2 as shown in the figure. The light suffers zero net deviation when it emerges into air from surface CD. If the angle of incidence (in degrees) is 5n. Find n ?
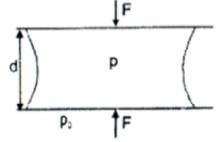
A drop water of mass m = 4.0 g is placed between two clean glass plates, the distance between the plates is 0.01cm. Find the force (103N) required to pull the plates away. Surface tension of water = 0.08 N/m and density of water is 1000 kg/m3
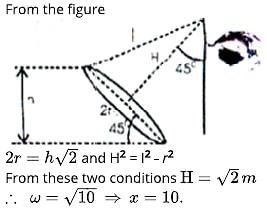
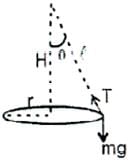
A car is accelerating horizontally with constant acceleration a=10m/s2. One end of a light string is attached to the roof of the ceiling and there is a small bob at other end of string. The bob is given an initial velocity such that it continues to move in uniform circular motion with respect to an observer inside the car. The bob moves such the maximum vertical separation between two points of its path is h=1m. The length of the string is 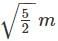 and acceleration due to gravity g=10m/s2. If the angular speed of the bob in rad/s is √x .find the value of x.
and acceleration due to gravity g=10m/s2. If the angular speed of the bob in rad/s is √x .find the value of x.
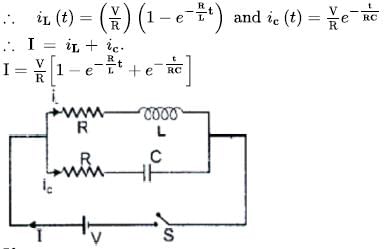
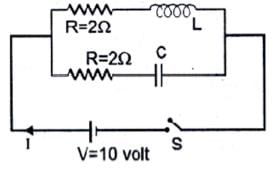
Find the current (in A) through the battery after the switch S is closed if L/R = RC = 1 ms.
Assuming that the law of gravitation is of the form 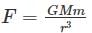 and attractive. A body of mass m revolves in a circular path of radius r around a fixed body of mass M. Find on what power of r will the square of time period depend.
and attractive. A body of mass m revolves in a circular path of radius r around a fixed body of mass M. Find on what power of r will the square of time period depend.
Place the following alcohols in decreasing order of rate of dehydration with concentrated H2SO4 :
1. CH3CH2CH(OH)CH2CH2CH3
2. (CH3)2C(OH)CH2CH2CH3
3. (CH3)2C(OH)CH(CH3)2
4. CH3CH2CH(OH)CH(CH3)2
5. CH3CH2CH2CH2CH2CH2OH
1.2 g of a salt with its empirical formula KxHy(C2O4)z was dissolved in 50 mL of water and its 10 mL portion required 11 mL of a 0.1 M HCl solution to reach the equivalence point. In a separate titration, 15 mL of the stock solution required 20 mL 0.2475 M KOH to reach the equivalence point. Identify the correct option.
In nitroprusside ion the iron and NO exist as Fe II and NO+ rather than Fe III and NO. These forms can be differentiated by
Among the following pair of oxides, which pair cannot be reduced by carbon to give the respective metals ?
|
357 docs|148 tests
|
|
357 docs|148 tests
|


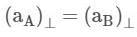
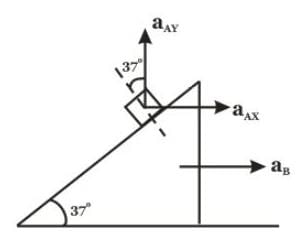

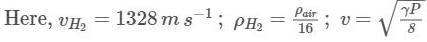
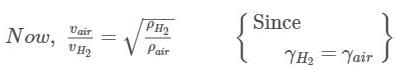
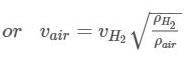
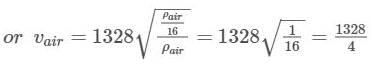
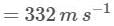

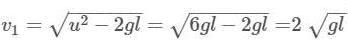
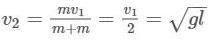
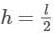
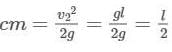
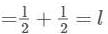

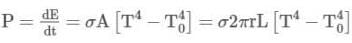
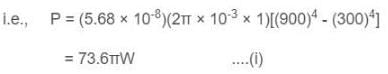
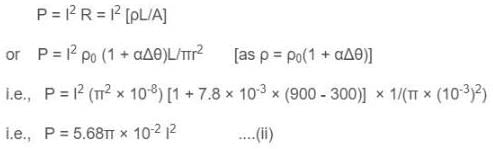
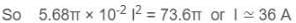
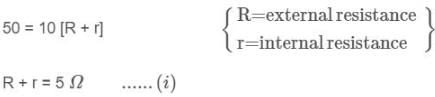
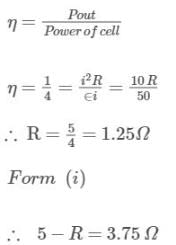

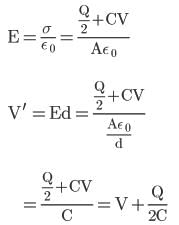
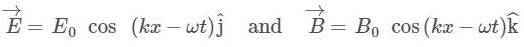
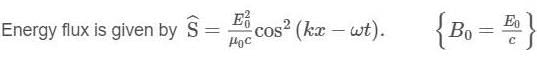
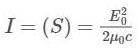
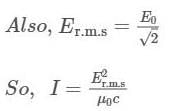
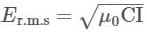
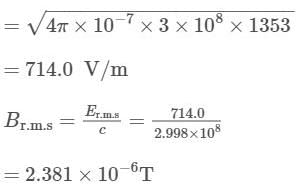
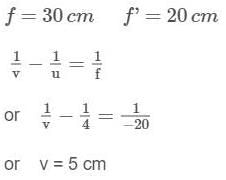
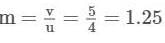


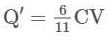
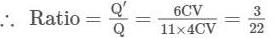
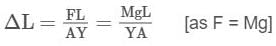


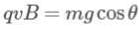
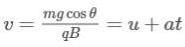 (along the inclined plane)
(along the inclined plane)
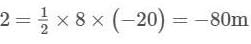 Which means it moves towards left.
Which means it moves towards left.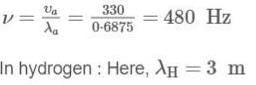
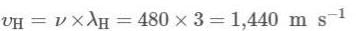
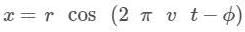 ... (ii)
... (ii)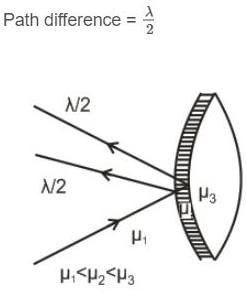
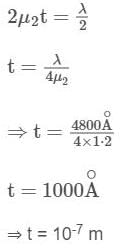
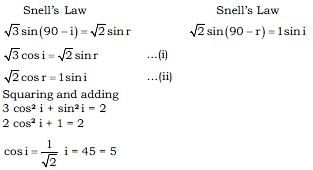
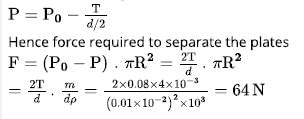
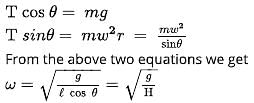
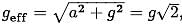 inclined at an angle of 450 with the verticle axis.
inclined at an angle of 450 with the verticle axis.