Test: Linear Programming (CBSE Level) - 1 - JEE MCQ
25 Questions MCQ Test Mathematics (Maths) Class 12 - Test: Linear Programming (CBSE Level) - 1
In a LPP, the objective function is always
Maximize Z = – x + 2y, subject to the constraints: x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Two godowns A and B have grain capacity of 100 quintals and 50 quintals respectively. They supply to 3 ration shops, D, E and F whose requirements are 60, 50 and 40 quintals respectively. The cost of transportation per quintal from the godowns to the shops are given in the following table:

How should the supplies be transported in order that the transportation cost is minimum? What is the minimum cost?
How should the supplies be transported in order that the transportation cost is minimum? What is the minimum cost?
Corner points of the feasible region for an LPP are (0, 2), (3, 0), (6, 0), (6, 8) and (0, 5). Let F = 4x + 6y be the objective function. Maximum of F – Minimum of F =
A linear programming problem is one that is concerned with
Which of the following types of problems cannot be solved by linear programming methods
The optimal value of the objective function Z = ax + by may or may not exist, if the feasible region for a LPP is
One kind of cake requires 200g of flour and 25g of fat, and another kind of cake requires 100g of flour and 50g of fat. Find the maximum number of cakes which can be made from 5kg of flour and 1 kg of fat assuming that there is no shortage of the other ingredients used in making the cakes.
An oil company has two depots A and B with capacities of 7000 L and 4000 L respectively. The company is to supply oil to three petrol pumps, D, E and F whose requirements are 4500L, 3000L and 3500L respectively. The distances (in km) between the depots and the petrol pumps is given in the following table:
Assuming that the transportation cost of 10 litres of oil is Re 1 per km, how should the delivery be scheduled in order that the transportation cost is minimum?What is the minimum cost?
Corner points of the feasible region determined by the system of linear constraints are (0, 3), (1, 1) and (3, 0). Let Z = px+qy, where p, q > 0. Condition on p and q so that the minimum of Z occurs at (3, 0) and (1, 1) is
In linear programming feasible region (or solution region) for the problem is
In a LPP if the objective function Z = ax + by has the same maximum value on two corner points of the feasible region, then every point on the line segment joining these two points give the same
A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftman’s time in its making while a cricket bat takes 3 hour of machine time and 1 hour of craftman’s time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftsman’s time. What number of rackets and bats must be made if the factory is to work at full capacity?
A fruit grower can use two types of fertilizer in his garden, brand P and brand Q. The amounts (in kg) of nitrogen, phosphoric acid, potash, and chlorine in a bag of each brand are given in the table. Tests indicate that the garden needs at least 240 kg of phosphoric acid, at least 270 kg of potash and at most 310 kg of chlorine.If the grower wants to minimise the amount of nitrogen added to the garden, how many bags of each brand should be used? What is the minimum amount of nitrogen added in the garden? should the delivery be scheduled in order that the transportation cost is minimum?
In a LPP, the linear inequalities or restrictions on the variables are called
In linear programming infeasible solutions
In linear programming problems the function whose maxima or minima are to be found is called
A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftman’s time in its making while a cricket bat takes 3 hour of machine time and 1 hour of craftman’s time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftsman’s time. If the profit on a racket and on a bat is Rs 20 and Rs 10 respectively, find the maximum profit of the factory when it works at full capacity?
A fruit grower can use two types of fertilizer in his garden, brand P and brand Q. The amounts (in kg) of nitrogen, phosphoric acid, potash, and chlorine in a bag of each brand are given in the table. Tests indicate that the garden needs at least 240 kg of phosphoric acid, at least 270 kg of potash and at most 310 kg of chlorine.
If the grower wants to maximise the amount of nitrogen added to the garden, how many bags of each brand should be added? What isthe maximum amount of nitrogen added?
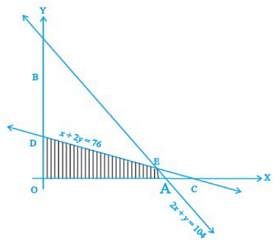
Determine the maximum value of Z = 3x + 4y if the feasible region (shaded) for a LPP is shown in Figure above.
In linear programming, optimal solution
In linear programming problems the optimum solution
A manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of Rs17.50 per package on nuts and Rs 7.00 per package on bolts. How many packages of each should be produced each day so as to maximise his profit, if he operates his machines for at the most 12 hours a day?
A toy company manufactures two types of dolls, A and B. Market tests and available resources have indicated that the combined production level should not exceed 1200 dolls per week and the demand for dolls of type B is at most half of that for dolls of type A. Further, the production level of dolls of type A can exceed three times the production of dolls of other type by at most 600 units. If the company makes profit of Rs 12 and Rs 16 per doll respectively on dolls A and B, how many of each should be produced weekly in order to maximise the profit?
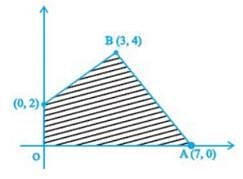
Feasible region (shaded) for a LPP is shown in Figure. Maximize Z = 5x + 7y.
|
204 videos|290 docs|139 tests
|
|
204 videos|290 docs|139 tests
|

















