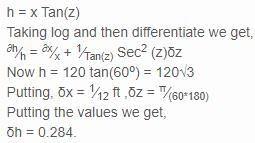All Courses
Get the App Signup / Login
Sign in Open App
JEE Exam  >  JEE Tests  >  Mathematics (Maths) Class 12  >  Test: Rate of Change And Approximations - JEE MCQ

Test: Rate of Change And Approximations - JEE MCQ


Test Description

10 Questions MCQ Test Mathematics (Maths) Class 12 - Test: Rate of Change And Approximations

Test: Rate of Change And Approximations for JEE 2024 is part of Mathematics (Maths) Class 12 preparation. The Test: Rate of Change And Approximations questions and answers have been prepared according to the JEE exam syllabus.The Test: Rate of Change And Approximations MCQs are made for JEE 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Rate of Change And Approximations below.
Solutions of Test: Rate of Change And Approximations questions in English are available as part of our Mathematics (Maths) Class 12 for JEE & Test: Rate of Change And Approximations solutions in Hindi for Mathematics (Maths) Class 12 course. Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free. Attempt Test: Rate of Change And Approximations | 10 questions in 10 minutes | Mock test for JEE preparation | Free important questions MCQ to study Mathematics (Maths) Class 12 for JEE Exam | Download free PDF with solutions
Test: Rate of Change And Approximations - Question 1
Save

The radius of air bubble is increasing at the rate of 0. 25 cm/s. At what rate the volume of the bubble is increasing when the radius is 1 cm.​

Test: Rate of Change And Approximations - Question 2
Save

The total revenue in Rupees received from the sale of x units of a product is given by R(x) = 5x2 + 22x + 35. Find the marginal revenue, when x = 7, where by marginal revenue we mean the rate of change of total revenue with respect to the number of items sold at an instant

Detailed Solution for Test: Rate of Change And Approximations - Question 2

1 Crore+ students have signed up on EduRev. Have you? Download the App
Test: Rate of Change And Approximations - Question 3
Save

Find the approximate change in total surface area of a cube of side x metre caused by increase in side by 1%.​

Test: Rate of Change And Approximations - Question 4
Save

The volume of cube is increasing at the constant rate of 3 cm3/s. Find the rate of change of edge of the cube when its edge is 5 cm.​
Detailed Solution for Test: Rate of Change And Approximations - Question 4

Let V be the instantaneous volume of the cube.
dV/dt = 3 cm3/s
Let x be the side of the cube.
V = x3
dV/dt = 3x2 * (dx/dt)
3 = 3*(52)*(dx/dt)
So, dx/dt = 1/25 cm/s

Test: Rate of Change And Approximations - Question 5
Save

The total cost associated with the production of x units of a product is given by C(x) = 5x2 + 14x + 6. Find marginal cost when 5 units are produced
Detailed Solution for Test: Rate of Change And Approximations - Question 5

C(x) = 5x2 + 14x + 6
Marginal Cost M(x) = C’(x)
M(x) = 10x +14
So, M(5) = 50 + 14
= 64 Rs

Test: Rate of Change And Approximations - Question 6
Save

At a distance of 120ft from the foot of a tower the elevation of its top is 60o. If the possible error in measuring the distance and elevation are 1 inch and 1 minute, find approximate error in calculated height.
Detailed Solution for Test: Rate of Change And Approximations - Question 6

Tan(z) = h⁄x

Test: Rate of Change And Approximations - Question 7
Save

A stone is dropped into a quiet lake and waves move in circles at a speed of 2cm per second. At the instant, when the radius of the circular wave is 12 cm, how fast is the enclosed area changing ?​
Detailed Solution for Test: Rate of Change And Approximations - Question 7

Rate of increase of radius dr/dt = 2 cm/s
Area of circle A = πr2
dA/dt = π*(2r)*(dr/dt)
= π*(24)*2
= 48π cm2/s
Rate of increase of area is 48π cm2/s (increasing as it is positive).

Test: Rate of Change And Approximations - Question 8
Save

Using approximation find the value of  ​
Detailed Solution for Test: Rate of Change And Approximations - Question 8

Let x=4, Δx=0.01

y=x^½ = 2

y+Δy = (x+ Δx)^½ = (4.01)^½

Δy = (dy/dx) * Δx

Δy = (x^(-1/2))/2 * Δx

Δy = (½)*(½) * 0.01

Δy = 0.25 * 0.01

Δy = 0.0025

So, (4.01)^½ = 2 + 0.0025 = 2.0025

Test: Rate of Change And Approximations - Question 9
Save

Find the approximate value of f(10.01) where f(x) = 5x2 +6x + 3​
Detailed Solution for Test: Rate of Change And Approximations - Question 9

f(x) = 5x2 +6x + 3
f(10.01) = 5*(10.01)2 + 6*(10.01) + 3
To find (10.01)2
Let p=10, Δp=0.01
y=p2 = 100
y+Δy = (p+ Δp)2 = (10.01)2
Δy = (dy/dp) * Δp
Δy = 2*p* Δx
Δy = 2*10* 0.01
Δy = 20 * 0.01
Δy = 0.2
So, (10.01)2 = y + Δy
= 100.2
So,
f(10.01) = 5*(100.2) + 6*(10.01) + 3
= 501 + 60.06 + 3
= 564.06

Test: Rate of Change And Approximations - Question 10
Save

Given a function y = f(x) . Let Δx be the very small change in the value of x , then the corresponding change in the value of y that is Δy is approximately given by
204 videos|290 docs|139 tests
Join Course
Information about Test: Rate of Change And Approximations Page
In this test you can find the Exam questions for Test: Rate of Change And Approximations solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Rate of Change And Approximations, EduRev gives you an ample number of Online tests for practice

Top Courses for JEE

204 videos|290 docs|139 tests
Join Course
Download as PDF

Top Courses for JEE

Important Questions for Rate of Change And Approximations

Find all the important questions for Rate of Change And Approximations at EduRev.Get fully prepared for Rate of Change And Approximations with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Rate of Change And Approximations syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Rate of Change And Approximations resources.

Rate of Change And Approximations MCQs with Answers

Prepare for the Rate of Change And Approximations within the JEE exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Rate of Change And Approximations Mathematics (Maths) Class 12

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Rate of Change And Approximations with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup