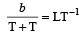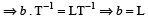31 Year NEET Previous Year Questions: Units & Measurement - NEET MCQ
30 Questions MCQ Test Physics Class 11 - 31 Year NEET Previous Year Questions: Units & Measurement
The dimensional formula for angular momentum is [1988]
If C and R denote capacitance and resistance, the dimensional formula of CR is [1988]
The dimensional formula of torque is [1989]
Dimensional formula of self inductance is [1989]
Of the following quantities, which one has dimension different from the remaining three? [1989]
If x = at + bt2, where x is the distance travelled by the body in kilometers while t is the time in seconds, then the units of b is [1989]
According to Newton, the viscous force acting between liquid layers of area A and velocity gradient ΔV/ΔZ is given by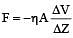 where η is constant called coefficient of viscosity. The dimensional formula of η is [1990]
where η is constant called coefficient of viscosity. The dimensional formula of η is [1990]
The frequency of vibration f of a mass m suspended from a spring of spring constant k is given by a relation of the type f = c mx ky, where c is a dimensionless constant. The values of x and y are
The dimensional formula of pressure is [1990]
The dimension al formula for permeability µ is given by [1991]
A certain body weighs 22.42 gm and has a measured volume of 4.7 cc. The possible error in the measurement of mass and volume are 0.01 gm and 0.1 cc. Then maximum error in the den sity will be [1991]
P represents radiation pressure, crepresents speed of light and Q represents radiation energy striking unit area per sec. The non zero integers x, y, z such that Px Qy cz is dimensionless are [1992]
The time dependence of a physical quantity p is given by p = p0 exp (– αt2), where α is a constant and t is the time. The constant α [1993]
urpentine oil is flowing through a tube of length l and radius r. The pressure difference between the two ends of the tube is P. The viscosity of oil is given by  where v is the velocity of oil at a distance a from the axis of the tube. The dimensions of η are
where v is the velocity of oil at a distance a from the axis of the tube. The dimensions of η are
In a vernier calliper N divisions of vernier scale coincides with (N – 1) divisions of main scale (in which length of one division is 1 mm). The least count of the instrument should be[1994]
In a particular system, the unit of length, mass and time are chosen to be 10 cm, 10 g and 0.1 s respectively. The unit of force in this system will be equivalen t to [1994]
Which of the following is a dimensional constant? [1995]
The percentage errors in the measurement of mass and speed are 2% and 3% respectively.The error in kinetic energy obtained by measuring mass and speed will be [1995]
An equation is given as : 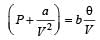
where P = Pressure, V = Volume & θ = Absolute temperature. If a and b are constants, then dimensions of a will be [1996]
The density of a cube is measured by measuring its mass and length of its sides. If the maximum error in the measurement of mass and length are 4% and 3% respectively, the maximum error in the measurement of den sity will be [1996]
Which of the following will have the dimensions of time [1996]
The force F on a sphere of radius a moving in a medium with velocity v is given by F = 6πηav.The dimensions of η are [1997]
The dimensional formula for magnetic flux is [1999]
Which one of the following groups have quantities that do not have the same dimensions? [2000]
The dimensions of Planck’s constant are same as [2001]
The unit of the Stefan-Boltzmann's constant is [2002]
The unit of permittivity of free space, εo is [2004]
The dimensions of universal gravitational constant are [1992, 2004]
The ratio of the dimension of Planck’s constant and that of the moment of inertia has the dimension of [2005]
The velocity v of a particle at time t is given by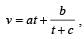 where a, b and c are constant.The dimensions of a, b and c are respectively [2006]
where a, b and c are constant.The dimensions of a, b and c are respectively [2006]
|
97 videos|379 docs|103 tests
|



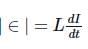
 is the rate of change of current.
is the rate of change of current.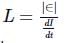
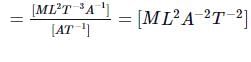


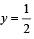
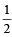
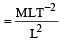 = ML–1T–2
= ML–1T–2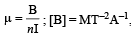
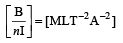
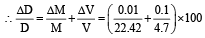 =2 %
=2 %
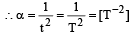
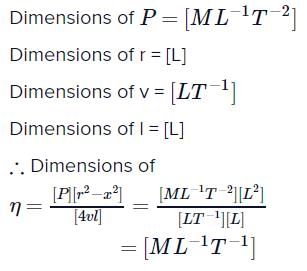
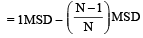
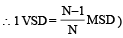
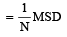
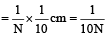
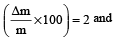
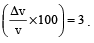
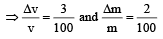
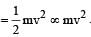
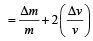
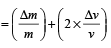
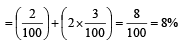

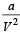
 = Dimension of
= Dimension of 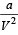
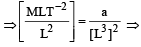 a = [M L5 T–2]
a = [M L5 T–2]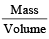
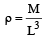
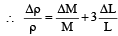
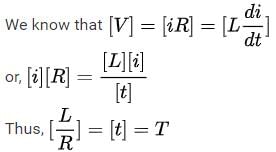
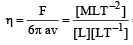 = ML–1T–1
= ML–1T–1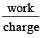
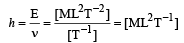
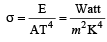
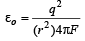
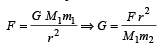
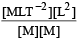

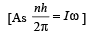
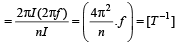
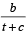 = Dimension of v
= Dimension of v