Test: Gravitation - NEET MCQ
30 Questions MCQ Test Physics Class 11 - Test: Gravitation
To complete one revolution around Earth, communication satellites take
The height above surface of earth where the value of gravitational acceleration is one fourth of that at surface, will be
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The decrease in the value of g on going to a height R/2 above the earth's surface will be
At what altitude will the acceleration due to gravity be 25% of that at the earth's surface (given radius of earth is R) ?
If the rotational motion of earth increases, then the weight of the body -
On doubling the distance between two masses the gravitational force between them will -
If the acceleration due to gravity inside the earth is to be kept constant, then the relation between the density d and the distance r from the centre of earth will be -
Let w be the angular velocity of the earth's rotation about its axis. Assume that the acceleration due to gravity on the earth's surface has the same value at the equator and the poles. An object weighed at the equator gives the same reading as a reading taken at a depth d below earth's surface at a pole (d << R). The value of d is
If the radius of the earth be increased by a factor of 5, by what factor its density be changed to keep the value of g the same ?
The mass and diameter of a planet are twice those of earth. What will be the period of oscillation of a pendulum on this planet if it is a seconds pendulum on earth ?
A particle of mass M is at a distance a from surface of a thin spherical shell of equal mass and having radius a.
If the kinetic energy of a satellite orbiting around the earth is doubled then -
The escape velocity from a planet is v0. The escape velocity from a planet having twice the radius but same density will be -
Two planets A and B have the same material density. If the radius of A is twice that of B, then the ratio of the escape velocity is
A hollow spherical shell is compressed to half its radius. The gravitational potential at the centre
A (nonrotating) star collapses onto itself from an initial radius Ri with its mass remaining unchanged. Which curve in figure best gives the gravitational acceleration ag on the surface of the star as a function of the radius of the star during the collapse ?
A satellite of the earth is revolving in circular orbit with a uniform velocity V. If the gravitational force suddenly disappears, the statellite will
A satellite revolves in the geostationary orbit but in a direction east to west. The time interval between its successive passing about a point on the equator is
Two point masses of mass 4m and m respectively separated by d distance are revolving under mutual force of attraction. Ratio of their kinetic energies will be
with the orbit radius of a body in circular planetary motion. Find the correct state ment about the
curves A, B and C
Two different masses are dropped from same heights, then just before these strike the ground, the following is same :
When a satellite moves around the earth in a certain orbit, the quantity which remains constant is
A body of mass m rises to height h = R/5 from the earth's surface, where R is earth's radius. If g is acceleration due to gravity at earth's surface, the increase in potential energy is
A planet has mass 1/10 of that of earth, while radius is 1/3 that of earth. If a person can throw a stone on earth surface to a height of 90m, then he will be able to throw the stone on that planet to a height
Work done in taking a body of mass m to a height nR above surface of earth will be :
(R = radius of earth)
The potential energy of a body of mass 3kg on the surface of a planet is 54 joule. The escape velocity will be -
A body of mass m is situated at a distance 4Re above the earth's surface, where Re is the radius of earth. How much minimum energy be given to the body so that it may escape -
A satellite of earth is moving in its orbit with a constant speed v. If the gravity of earth suddenly vanishes, then this satellite will -
The ratio of distances of satellites A and B from the centre of the earth is 1.4 : 1, then the ratio of energies of satellites B and A will be –
|
97 videos|378 docs|103 tests
|



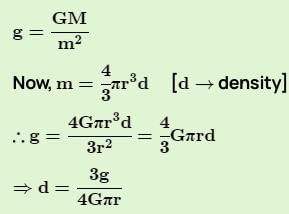 = d μ 1/r
= d μ 1/r
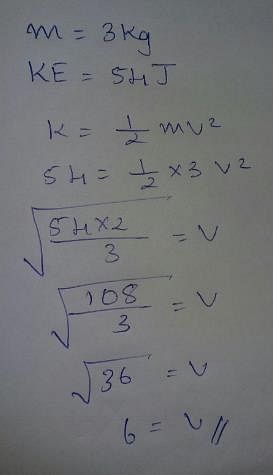
 Hence the ratio of total energy is in the inverse ratio of the distance ‘r’.
Hence the ratio of total energy is in the inverse ratio of the distance ‘r’.














