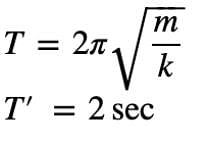Test: Oscillations - NEET MCQ
30 Questions MCQ Test Topic-wise MCQ Tests for NEET - Test: Oscillations
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The kinetic energy of a body executing S.H.M. is 1/3 of the potential energy. Then, the displacement of the body is x percent of the amplitude, where x is
If the length of a simple pendulum is increases by 1percent, then the new time-period
A body is executing S.H.M When its displacement from the mean position is 4 cm and 5 cm, the corresponding velocities of the body are 10 cm per sec and 8 cm per sec. Then the time period of the body is
A spring with spring constant k when stretched through 1 cm has a potential energy U. If it is stretched by 4 cm, the potential energy will become
Two pendulums have time periods T and 5T/4. They are in phase at their mean positions at some instant of time. What will be their phase difference when the bigger pendulum completes one oscillation?
The ratio of maximum acceleration to maximum velocity of a particle performing S.H.M is equal to
Two pendulums of length 1 m and 16 m start vibrating one behind the other from the same stand. At some instant, the two are in the mean position in the same phase. The time period of shorter pendulum is T. The minimum time after which the two threads of the pendulum will be one behind the other is
A particle is executing S.H.M with an amplitude of 4 cm and time period 12 sec. The time taken by the particle in going from its mean position to a position of displacement equal to 2 cm is T1..The time taken from this displaced position of 2 cm to reach the extreme position is T2. Therefore, T1/ T2 will be
Period of a periodic motion is the ________ interval of time after which the motion is __________.
For all practical purposes, the motion of a simple pendulum is SHM,
If the period of oscillation of mass M suspended from a spring is one second, then the period of mass 4 M will be
A rubber ball with water, having a small hole in its bottom is used as the bob of a simple pendulum. The time-period of such a pendulum:
A particle executes S.H.M. having time period T, then the time period with which the potential energy changes is:
The length of the second’s pendulum on the surface of earth is 1m. The length of second’s pendulum on the surface of moon, where g is 1/6th the value on earth is
In forced oscillations apart from acceleration forces, damping and spring forces there is
A mass M is suspended from a spring of negligible mass. The spring is pulled a little and then released so that the mass executes simple harmonic oscillations with a time period T. If the mass is increased by m, the time period becomes 5T/3. then the ratio of m/M is
The length of a second’s pendulum decreases by 0.1percent, then the clock
If the maximum velocity and acceleration of a particle executing S.H.M are equal in magnitude, the time period will be
|
9 docs|1272 tests
|