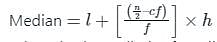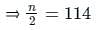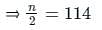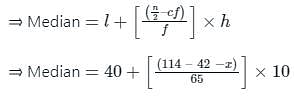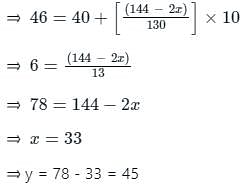Test: Measures of Central Tendency - 1 - SSC CGL MCQ
10 Questions MCQ Test Statistics for SSC CGL - Test: Measures of Central Tendency - 1
The median of numbers 10, 8, 2, 7, 3, 8, 5, 1 is k. If 10 is replaced by 1, then new median is r. The value of (k - r) is:
Let x, y, z are three observations. The mean of these observations is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In the following distribution, the value of median is 46, and x + y = 78 then the values of x and y are :

If mean of 14, 13, 18, 16, k, (k + 3) is 13, then what will be the mean of k, 8, 9, 11, 5, 10, 6?
What is the mode of 8, 5, 7, 10, 15, 21, 5, 7, 2, 5?
Construction of a cumulative frequency table is useful in determining the:
If the mean of 10 numbers is 96 and one of the numbers is 150, then what is the mean of the remaining nine numbers?
Below are the results of the students in an exam. Find the mode of given results.
90, 80, 77, 86, 90, 91, 77, 25, 45, 35, 66, 69, 65, 43, 65, 75, 43, 90, 89.
Find the median of 4.1, 5.2, 6.3, 3.6, 2.4, 6.4, 4.6
|
72 videos|87 docs|18 tests
|
|
72 videos|87 docs|18 tests
|