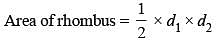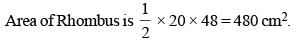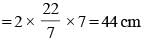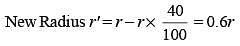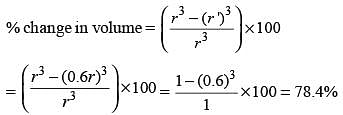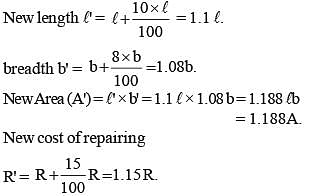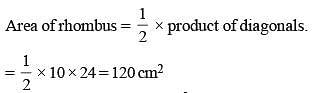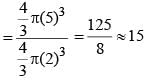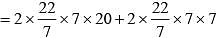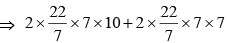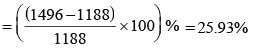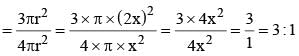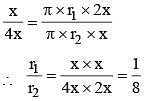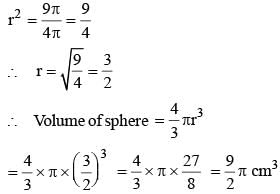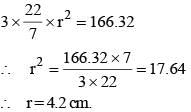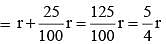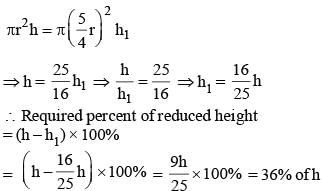SSC CGL Previous Year Questions: Mensuration - 1 - SSC CGL MCQ
20 Questions MCQ Test SSC CGL Mathematics Previous Year Paper (Topic-wise) - SSC CGL Previous Year Questions: Mensuration - 1
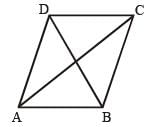
The length of one of the diagonals of a rhombus is 48 cm. If the side of the rhombus is 26 cm, then what is the area of the rhombus? (SSC MTS 2018)
The edge of a cube is 8 cm. What is the total surface area of the cube? (SSC MTS 2018)
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
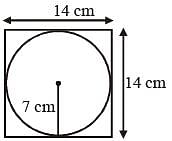
What is the circumference of the largest circle which can be inscribed in a square of side 14 cm? (Take π = 22/7) (SSC MTS 2018)
Five cubes, each of edge 3 cm are joined end to end. What is the total surface area of the resulting cuboid, in cm2? (SSC CGL-2018)
The radius of a sphere is reduced by 40%. By what percent will its volume decrease? (SSC CGL-2018)
A rectangular portion of an airport runway was getting repaired for which an estimate was made on the basis of a rate ₹ R per square unit. But while doing the work, the length of the portion got increased by 10% and the breadth by 8%. Over and above this, there was an increase in the cost of the repair work to the extent of 15%. What was the overall percentage increase in the cost of repair over the estimate? (SSC CHSL-2018)
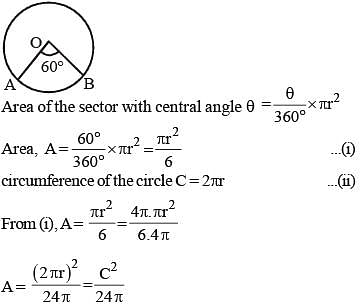
The area of a sector of a circle with central angle 60º is A. The circumference of the circle is C. Then A is equal to: (SSC CHSL-2018)
The radius of a cylinder is increased by 120% and its height is decreased by 40%. What is the percentage increase in its volume? (SSC Sub. Ins. 2018)
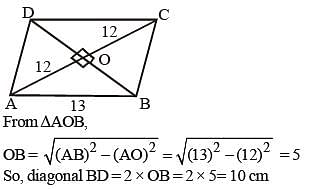
One side of a rhombus is 13 cm and one of its diagonals is 24 cm. What is the area of the rhombus? (SSC Sub. Ins. 2018)
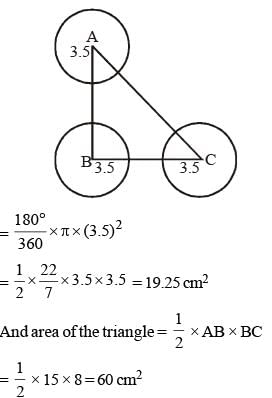
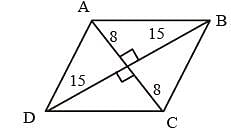
The sides of a triangle are 8 cm, 15 cm and 17 cm respectively. At each of its vertices, circles of radius 3.5 cm are drawn. What is the area of the triangle excluding the portion covered by the sectors of the circles (π = 22/7)? (SSC Sub. Ins. 2018)
A sphere of radius 5 cm is melted and recast into spheres of radius 2 cm each. How many such spheres can be made? (SSC Sub. Ins. 2018)
6 cubes, each of edge 4 cm, are joined end to end. What is the total surface area of the resulting cuboid? (SSC Sub. Ins. 2018)
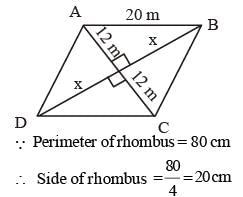
If the perimeter of a rhombus is 80 cm and one of its diagonal is 24 cm, then what is the area (in cm2) of the rhombus? (SSC Sub. Ins. 2017)
A solid cylinder having radius of base as 7 cm and length as 20 cm is bisected from its height to get two identical cylinders.
What will be the percentage increase in the total surface area? (SSC Sub. Ins. 2017)
Radius of hemisphere is twice that of a sphere. What is the ratio of total surface area of hemisphere and sphere? (SSC Sub. Ins. 2017)
The ratio of curved surface area of two cones is 1 : 4 and the ratio of slant height of the two cones is 2 : 1. What is the ratio of the radius of the two cones? (SSC Sub. Ins. 2017)
If diagonals of a rhombus are 16 cm and 30 cm. then what is the perimeter (in cm) of the rhombus? (SSC Sub. Ins. 2017)
A sphere has a total surface area 9 π cm2. Its volume is: (SSC MTS 2017)
The total surface area of a hemisphere is 166.32 sq cm, find its radius? (SSC CHSL 2017)
If the radius of the cylinder is increased by 25%, then by how much percent the height must be reduced, so that the volume of the cylinder remains same? (SSC CGL 2017)
|
21 docs|55 tests
|
|
21 docs|55 tests
|