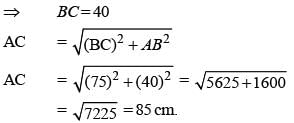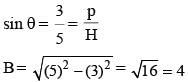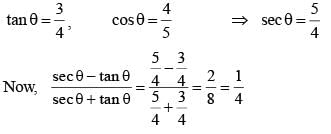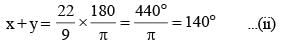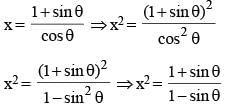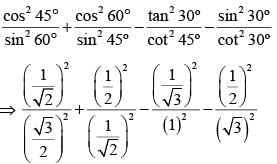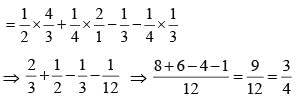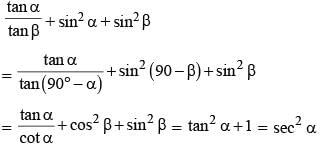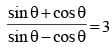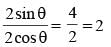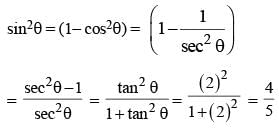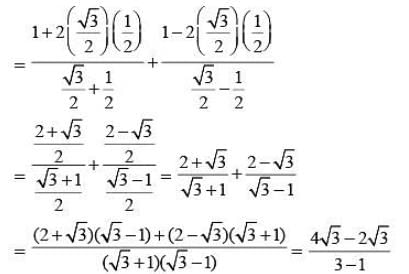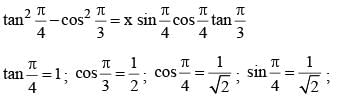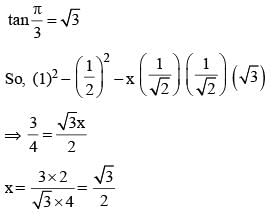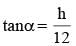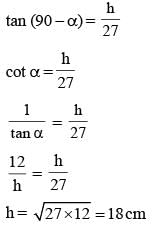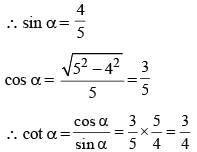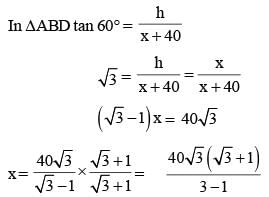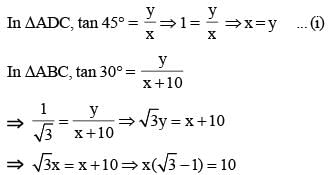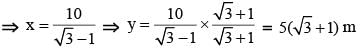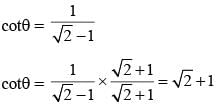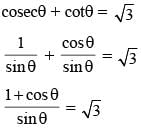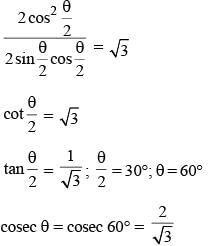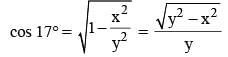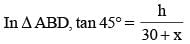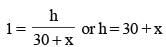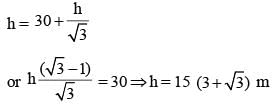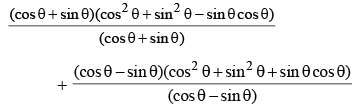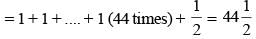SSC CGL Previous Year Questions: Trigonometry - 3 - SSC CGL MCQ
30 Questions MCQ Test - SSC CGL Previous Year Questions: Trigonometry - 3
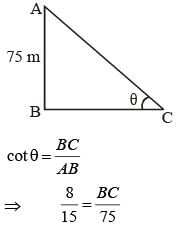
A kite is flying at the height of 75 m from the ground. The string makes an angle q (where cot θ = 8/15) with the level ground. Assuming that there is no slack in the string, the length of the string is equal to: (SSC CGL 1st Sit. 2015)
If 5 sin θ = 3, the numerical value of 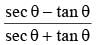 (SSC CGL 1st Sit. 2015)
(SSC CGL 1st Sit. 2015)
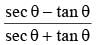 (SSC CGL 1st Sit. 2015)
(SSC CGL 1st Sit. 2015)If q be acute angle and tan (4θ – 50°) = cot (50° – θ), then the value of θ in degrees is: (SSC CGL 1st Sit. 2015)
The value of sin222° + sin268° + cot230° is (SSC CGL 1st Sit. 2015)
If the sum and difference of two angles are 22/9 radian and 36° respectively, then the value of smaller angle in degree taking the value of π as 22/ 7 is: (SSC CGL 1st Sit. 2015)
The minimum value of 2 sin2 θ + 3 cos2 θ is (SSC CGL 1st Sit. 2015)
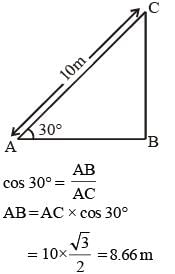
A 10 m long ladder is placed against a wall. It is inclined at an angle of 30° to the ground. The distance (in m) of the foot of the ladder from the wall is (Given √3 = 1.732) (SSC CGL 1st Sit. 2015)
If x cos θ – sin θ = 1, then x2 – (1 + x2) sin θ equals (SSC CGL 1st Sit. 2015)
The numerical value of 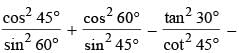
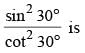 (SSC CGL 1st Sit. 2015)
(SSC CGL 1st Sit. 2015)
Find the value of tan 4° tan 43° tan 47° tan 86° (SSC CGL 1st Sit. 2015)
The maximum value of sin4θ + cos4θ is (SSC CGL 1st Sit. 2015)
If α + β = 90° then the expression 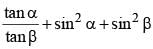 is equal to: (SSC CHSL 2015)
is equal to: (SSC CHSL 2015)
If sin 2θ = √3/2 then the value of sin 3θ is equal to: (take (0° ≤ θ ≤ 90°) (SSC CHSL 2015)
If 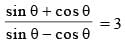 then the value of sin2θ is: (SSC CHSL 2015)
then the value of sin2θ is: (SSC CHSL 2015)
Value of the expression:
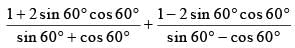 (SSC CHSL 2015)
(SSC CHSL 2015)
The value of x in the equation
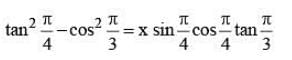 (SSC CHSL 2015)
(SSC CHSL 2015)
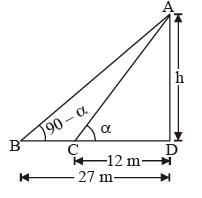
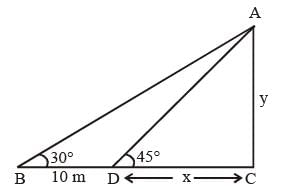
From two points on the ground and lying on a straight line through the foot of a pillar, the two angles of elevation of the top of the pillar are complementary to each other. If the distances of the two points from the foot of the pillar are 12 metres and 27 metres and the two points lie on the same side of the pillar, then the height (in metres) of the pillar is: (SSC Sub. Ins. 2015)
If sin θ + sin2 θ =1, then the value of cos2 θ + cos4 θ is: (SSC Sub. Ins. 2015)
If α is an acute angle and 2sin α + 15cos2 α = 7, then the value of cot α is: (SSC Sub. Ins. 2015)
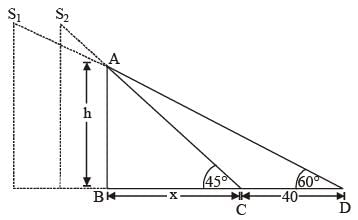
The shadow of a tower standing on a level plane is found to be 40m longer when the sun’s altitude is 45° than when it is 60°. The height of the tower is: (SSC Sub. Ins. 2015)
The length of the shadow of a vertical tower on level ground increases by 10 metres when the altitude of the sun changes from 45° to 30°. Then the height of the tower is (SSC CHSL 2014)
If sin θ + cos θ = √2 cos θ, then the value of cot θ is (SSC CGL 2014)
If cos α + sec α = √3, then the value of cos3 α + sec3 α is (SSC CGL 2014)
If θ is a positive acute angle and cosec θ + cot θ = √3, then the value of cosec θ is (SSC CGL 2014)
If sin 17° = x/y then sec 17° – sin 73° is equal to (SSC CGL 2014)
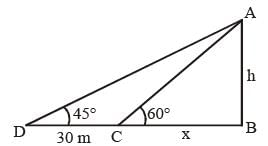
The shadow of a tower standing on a level plane is found to be 30 m longer when the Sun's altitude changes from 60° to 45°. The height of the tower is (SSC CGL 2014)
The value of 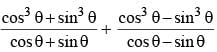 is equal to (SSC CGL 2014)
is equal to (SSC CGL 2014)
The value of sin21° + sin22° + sin23° + .... + sin289° is (SSC CGL 2014)
If (r cosθ - √3)2 + (r sinθ – 1)2 = 0, then the value of 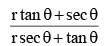 is equal to (SSC CHSL 2014)
is equal to (SSC CHSL 2014)
If θ is a positive acute angle and 4 cos2 θ – 4 cos θ + 1 = 0, then the value of tan (θ – 15°) is equal to (SSC CHSL 2014)