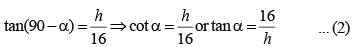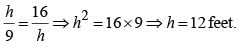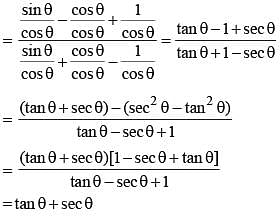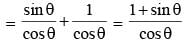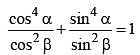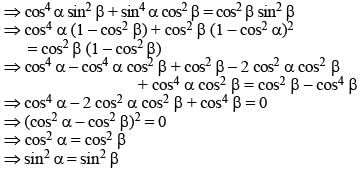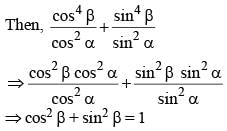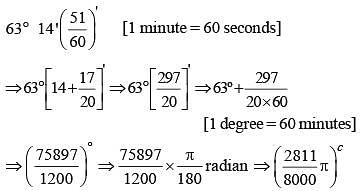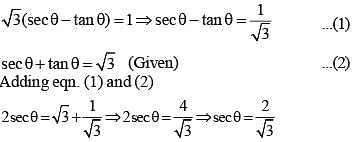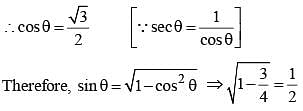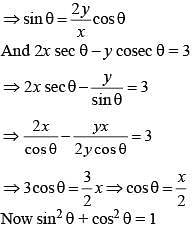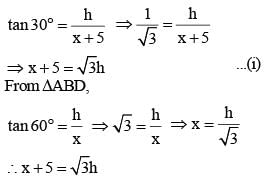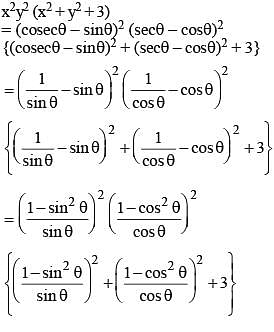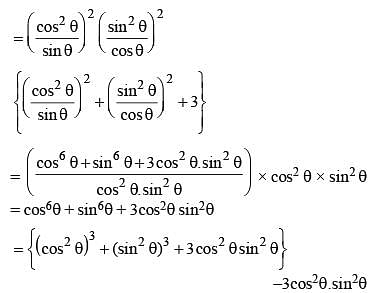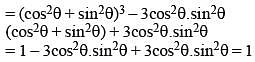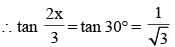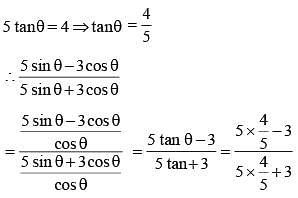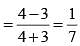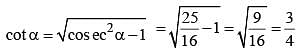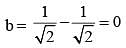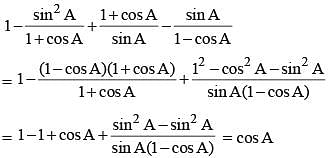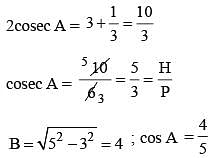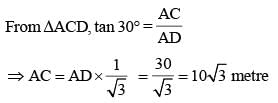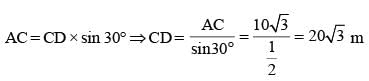SSC CGL Previous Year Questions: Trigonometry - 5 - SSC CGL MCQ
30 Questions MCQ Test SSC CGL Mathematics Previous Year Paper (Topic-wise) - SSC CGL Previous Year Questions: Trigonometry - 5
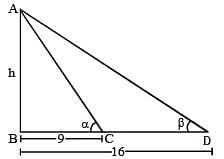
The angles of elevation of the top of a tower standing on a horizontal plane from two points on a line passing through the foot of the tower at a distance 9 ft and 16 ft respectively are complementary angles. Then the height of the tower is (SSC CGL 2nd Sit. 2012)
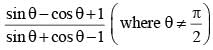 is equal to (SSC CGL 2nd Sit. 2012)
is equal to (SSC CGL 2nd Sit. 2012)
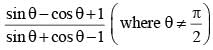 is equal to (SSC CGL 2nd Sit. 2012)
is equal to (SSC CGL 2nd Sit. 2012) | 1 Crore+ students have signed up on EduRev. Have you? Download the App |
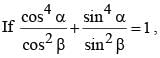 then the value of
then the value of 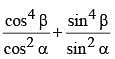 is (SSC CGL 2nd Sit. 2012)
is (SSC CGL 2nd Sit. 2012)
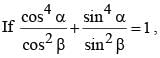 then the value of
then the value of 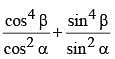 is (SSC CGL 2nd Sit. 2012)
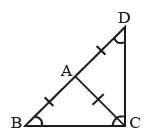
is (SSC CGL 2nd Sit. 2012)In a triangle ABC, AB = AC, BA is produced to D in such a manner that AC = AD. The circular measure of ∠BCD is (SSC CGL 2nd Sit. 2012)
The radian measure of 63°14'51" is (SSC CGL 2nd Sit. 2012)
If sec θ + tan θ = √3, then the positive value of sin θ is (SSC CGL 2nd Sit. 2012)
If 2y cos θ = x sin θ and 2x sec θ – y cosec θ = 3, then the relation between x and y is (SSC CGL 2nd Sit. 2012)
If sinθ + sin2θ = 1, then the value of cos12θ + 3cos10θ + 3cos8θ + cos6θ – 1 is (SSC CGL 1st Sit. 2012)
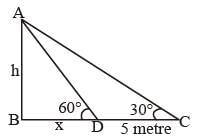
When the angle of elevation of the sum increases from 30° to 60°, the shadow of a post is diminished by 5 metres. then the height of the post is (SSC CGL 1st Sit. 2012)
If 0 ≤ 2 ≤ π/2, 2y cosθ = x sin θ and 2x secθ – y cosecθ = 3, then the value of x2 + 4y2 is (SSC CGL 1st Sit. 2012)
If x = cosecθ – sinθ and y = secθ – cosθ, then the value of x2y2 (x2 + y2 + 3) is (SSC CGL 1st Sit. 2012)
If tan (x + y) tan (x – y) = 1, then the value of tan (2x/3) is (SSC CGL 1st Sit. 2012)
The least value of (4sec2θ + 9 cosec2θ) is (SSC CGL 1st Sit. 2012)
If 5 tanθ = 4, then the value of 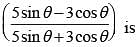 (SSC CGL 1st Sit. 2012)
(SSC CGL 1st Sit. 2012)
If x, y are positive acute angles, x + y < 90° and sin (2x – 20°) = cos (2y + 20°), then the value of sec (x + y) is (SSC CGL 2nd Sit. 2012)
If α is a positive acute angle and 2sinα + 15cos2α = 7, then the value of cotα is: (SSC CGL 2nd Sit. 2012)
If (a2 – b2) sinθ + 2ab cosθ = a2 + b2, then the value of tanθ is (SSC CGL 2nd Sit. 2012)
If tan θ – cot θ = a and cos θ – sin θ = b, then the value of (a2 + 4) (b2 – 1)2 is: (SSC CGL 2nd Sit. 2012)
If a3 – b3 = 56 and a – b = 2, then the value of (a2 + b2) is: (SSC CGL 2nd Sit. 2012)
The simplified value of 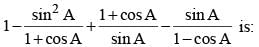 (SSC CGL 2nd Sit. 2012)
(SSC CGL 2nd Sit. 2012)
The least value of 4 cosec2α + 9sin2α is: (SSC CGL 2nd Sit. 2012)
If tan(x + y) tan (x – y) = 1, then the value of tan x is: (SSC CGL 2nd Sit. 2012)
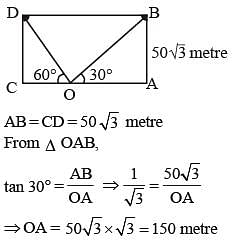
A boy standing in the middle of a field, observes a flying bird in the north at an angle of elevation of 30° and after 2 minutes, he observes the same bird in the south at an angle of elevation of 60°. If the bird flies all along in a straight line at a height of 50√3 m, then its speed in km/h is: (SSC CGL 2nd Sit. 2012)
In a right-angled triangle ABC, ∠B is the right angle and AC = 2√5 cm. If AB – BC = 2 cm, then the value of (cos2A – cos2C) is: (SSC CGL 2nd Sit. 2012)
If cot A + cosec A = 3 and A is an acute angle, then the value of cos A is: (SSC CGL 2nd Sit. 2012)
If cos A + cos2 A = 1, then sin2 A + sin4 A is equal to (SSC CGL 1st Sit. 2012)
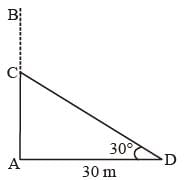
A tree is broken by the wind. If the top of the tree struck the ground at an angle of 30° and at a distance of 30 m from the root, then the height of the tree is (SSC CGL 1st Sit.2012)
sec4θ – sec2θ is equal to (SSC CGL 1st Sit. 2012)
If x sin3 θ + y cos3 θ = sin θ cos θ and x sin θ = y cos θ, sin θ ≠ 0, cos θ ≠ 0, then x2 + y2 is (SSC CGL 1st Sit. 2012)
If sin θ + cos θ = √2 cos (90° – θ), then cot θ is (SSC CGL 1st Sit. 2012)
|
21 docs|55 tests
|
|
21 docs|55 tests
|