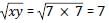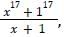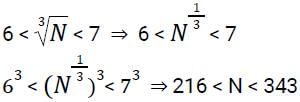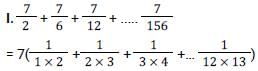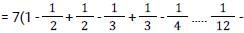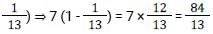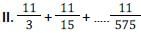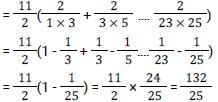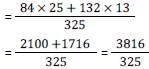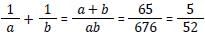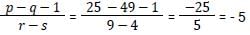Test: SSC CGL Previous Year Question: Number System and HCF & LCM (2023-2024) - 2 - SSC CGL MCQ
30 Questions MCQ Test SSC CGL Previous Year Papers - Test: SSC CGL Previous Year Question: Number System and HCF & LCM (2023-2024) - 2
What is the sum of all the common terms between the given series S1 and S2? [SSC CGL Tier II (08/08/2022)]
S1 = 2, 9, 16, ……., 632
S2 = 7, 11, 15, ……., 743
S1 = 2, 9, 16, ……., 632
S2 = 7, 11, 15, ……., 743
Three fractions x, y and z are such that x > y > z. When the smallest of them is divided by the greatest, the result is 9/16 which exceeds y by 0.0625. If x + y + z = 2(3/12), then what is the value of x + z? [SSC CGL Tier II (29/01/2022)]
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In finding the HCF of two numbers by division method, the last divisor is 17 and the quotients are 1, 11 and 2, respectively. What is the sum of the two numbers? [SSC CGL Tier II (13/09/2019)]
When 12, 16, 18, 20 and 25 divide the least number x, the remainder in each case is 4 but x is divisible by 7. What is the digit at the thousands’ place in x? [SSC CGL Tier II (11/09/2019)]
When an integer n is divided by 8, the remainder is 3. What will be the remainder if 6n - 1 is divided by 8? [SSC CGL 13/06/2019 (Evening)]
If a 11 digit number 5y5884805x6 is divisible by 72, where x = y, then the value of √xy is : SSC CGL 10/06/2019 (Morning)
An 11-digit number 7823326867X is divisible by 18. What is the value of X? [SSC CGL 19/07/2023 (1st shift)]
The sum of the two numbers is 98. The difference between the two numbers is 28, Find one of the two numbers. [SSC CGL 19/07/2023 (3rd shift)]
What is the sum of the divisors of 484 that are perfect squares? [SSC CGL 20/07/2023 (1st shift)]
What is the remainder when (x17 + 1) is divided by (x + 1)? [SSC CGL 25/07/2023 (3rd shift)]
A four-digits number abba is divisible by 4 and a < b. How many such numbers are there? [SSC CGL 26/07/2023 (1st shift)]
How many of the following numbers are divisible by 3 but NOT by 9? [SSC CGL 27/07/2023 (3rd shift)]
5826, 5964, 6039, 6336, 6489, 6564,6867 and 6960
Which number among 11368, 11638, 11863 and 12638 is divisible by 11? [SSC CGL 27/07/2023 (3rd shift)]
If the 5-digit number 750PQ is divisible by 3, 7 and 11, then what is the value of P + 2Q ? [SSC CGL 01/12/2022 (4th Shift)]
A number when divided by 7 leaves the remainder of 4. If the square of the same number is divided by 7, then what is the remainder? [SSC CGL 03/12/2022 (3rd Shift)]
On dividing a certain number by 363, we get 17 as the remainder. What will be the remainder when the same number is divided by 11? [SSC CGL 05/12/2022 (2nd Shift)]
The largest five-digit number which when divided by 7, 9 and 11, leaves the same remainder as 3 in each case, is: [ SSC CGL 05/12/2022 (2nd Shift)]
Find the greatest number that will divide 49, 147 and 322 to leave the same remainder in each case. [SSC CGL 06/12/2022 (1st Shift)]
The least number that should be added to 35460 so that the sum is exactly divisible by 3, 4, 5 and 7 is: [SSC CGL 12/12/2022 (1st Shift)]
A four-digit pin, say abcd, of a lock has different non-zero digits. The digits satisfy b = 2a, c = 2b, d = 2c. The pin is divisible by __________. [SSC CGL 13/12/2022 (2nd Shift)]
If lies between 6 and 7, where N is an integer then how many values N can take? [SSC CGL Tier II (08/08/2022)]
If the digits of a two digit number is reversed, then the number is decreased by 36. Which of the following is correct regarding the number? [SSC CGL Tier II (08/08/2022)]
I. The difference of the digits is 4.
II. The value of number can be 84.
III. Number is always a composite number.
x, y and z are distinct prime numbers where x < y < z. If x + y + z = 70 , then what is the value of z? [SSC CGL Tier II (08/08/2022)]
What is the value of 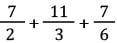
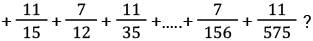 [SSC CGL Tier II (08/08/2022)]
[SSC CGL Tier II (08/08/2022)]
Find the greatest number 23a68b, which is divisible by 3 but NOT divisible by 9. [SSC CGL 11/04/2022 (Morning)]
Find the greatest number 234a5b, which is divisible by 22, but NOT divisible by 5. [SSC CGL 18/04/2022 (Morning)]
If the sum of two positive numbers is 65 and the square root of their product is 26, then the sum of their reciprocals is: [SSC CGL Tier II (29/01/2022)]
Let x = (433)24 - (377)32 + (166)54. What is the unit digit of x? [SSC CGL Tier II (29/01/2022)]
The sum of the digits of the least number which when divided by 36, 72, 80 and 88 leaves the remainders 16, 52, 60 and 68, respectively, is: [SSC CGL Tier II (03/02/2022)]
Let p, q, r and s be positive natural numbers having three exact factors including 1 and the number itself If q > p and both are two-digit numbers, and r > s and both are one-digit numbers, then the value of the expression 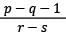 is: [SSC CGL Tier II (03/02/2022)]
is: [SSC CGL Tier II (03/02/2022)]
|
316 docs|268 tests
|


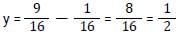
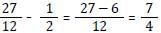 .
.