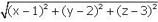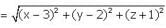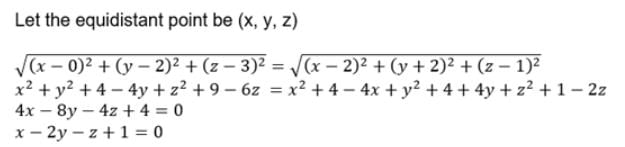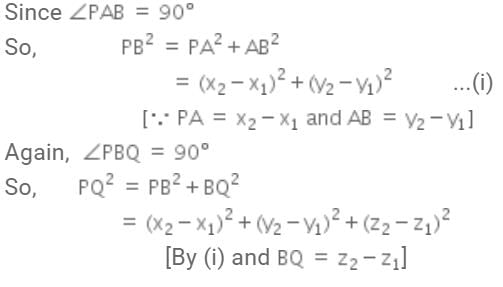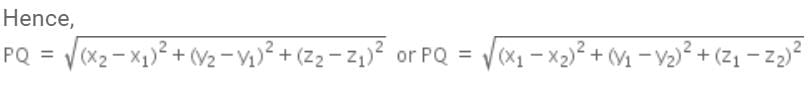Test: Distance Formula 3D Geometry - Commerce MCQ
10 Questions MCQ Test Mathematics (Maths) Class 11 - Test: Distance Formula 3D Geometry
The equation representing the set of points which are equidistant from the points (1, 2 , 3) and (3 , 2 , -1) is
The locus of the point which is equidistant from the points A(0, 2, 3) and B(2, -2, 1) is:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The distances of the point (1, 2, 3) from the coordinate axes are A, B and C respectively. Which option is correct?
A and B be the points (3, 4, 5) and (-1, -3, -7), respectively, the equation of the set of points P such that PA2 + PB2 = k2, where k is a constant will
A(4,7,8) B(2,3,4) , C (-1,-2,1) and D(1,2,5) are vertices of a quadrilateral. The quadrilateral is a
Find the points on z-axis which are at a distance 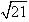 from the point (1, 2, 3).
from the point (1, 2, 3).
The distance of the point (3, 4, 5) from X-axis is:
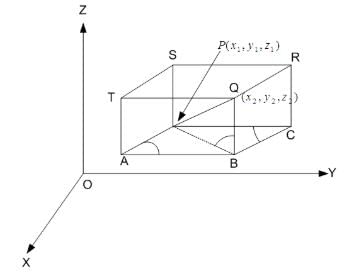
The distance between the points P(x1, y1, z1) and Q (x2, y2, z2) is given by:
The points (1, -1, 3), (2, -4, 5) and (5, -13, 11) are:
If P,Q,R be the mid points of sides AB, AC and BC of triangle ABC. Where , A (0, 0, 6), B (0,4, 0)and (6, 0, 0).Then
|
75 videos|238 docs|91 tests
|
|
75 videos|238 docs|91 tests
|