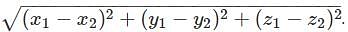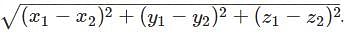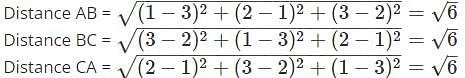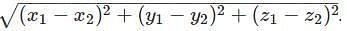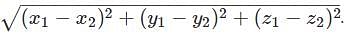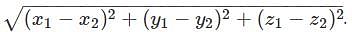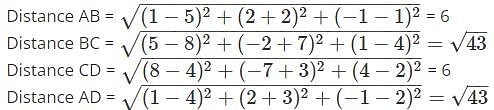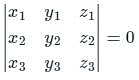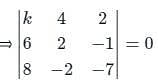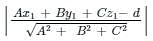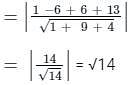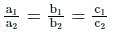Test: Distance between two points in 3D Space - SAT MCQ
10 Questions MCQ Test Mathematics for Digital SAT - Test: Distance between two points in 3D Space
Find the distance between two points (5, 6, 7) and (2, 6, 3).
The three points A (1, 2, 3), B (3, 1, 2), C (2, 3, 1) form _________.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The three points A (7, 0, 10), B (6, -1, 6), C (9, -4, 6) form ________.
The three points A (3, 0, 3), B (5, 3, 2), C (6, 5, 5) form ________.
The points A (1, 2, -1), B (5, -2, 1), C (8, -7, 4), D (4, -3, 2) form __________.
Find the cartesian equation of the plane which passes through the point (5, 2, -4) and perpendicular to the line with direction ratios 2, 3, -1?
If the points (k, 4, 2), (6, 2, - 1) and (8, - 2, - 7) are collinear, then find the value of k.
What is the distance of the point (1, 2, 3) form the plane x – 3y + 2z + 13 = 0?
Find the values of k so the line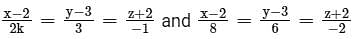 are parallel.
are parallel.
The sum of the direction cosine of z-axis is
|
185 videos|124 docs|75 tests
|
|
185 videos|124 docs|75 tests
|