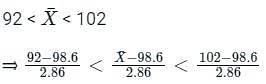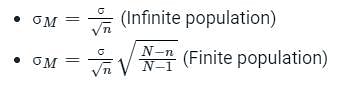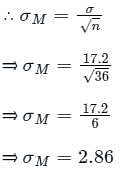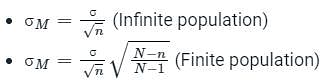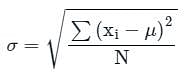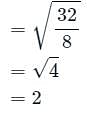Test: Statistics - ACT MCQ
15 Questions MCQ Test Mathematics for ACT - Test: Statistics
Comprehension:
Direction: Based on the following information, answer the questions.
For an experiment, a sample of 25 observations from normal distribution with mean 98.6 and s.d. 17.2 was selected. Answer the following questions:
What is P(92 < 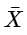 < 102)?
< 102)?
What is P(92 <
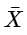 < 102)?
< 102)?Comprehension:
Direction: Based on the following information, answer the questions.
For an experiment, a sample of 25 observations from normal distribution with mean 98.6 and s.d. 17.2 was selected. Answer the following questions:
What is the standard error of mean, for the population size to be 100?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
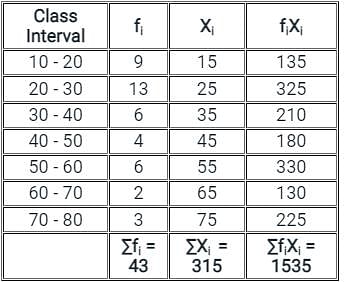
What is the mean of the range, mode and median of the data given below?
5, 10, 3, 6, 4, 8, 9, 3, 15, 2, 9, 4, 19, 11, 4
If mean and mode of some data are 4 & 10 respectively, its median will be:
Find the median of the given set of numbers 2, 6, 6, 8, 4, 2, 7, 9
The mean of four numbers is 37. The mean of the smallest three of them is 34. If the range of the data is 15, what is the mean of the largest three?
The data given below shows the marks obtained by various students.

What is the mean marks (Correct up to two decimal places) of given data?
Comprehension:
Direction: Based on the following information, answer the questions.
For an experiment, a sample of 25 observations from normal distribution with mean 98.6 and s.d. 17.2 was selected. Answer the following questions:
Find the corresponding probability given a sample of 36
Comprehension:
Direction: Based on the following information, answer the questions.
For an experiment, a sample of 25 observations from normal distribution with mean 98.6 and s.d. 17.2 was selected. Answer the following questions:
What is the standard error of mean for a sample size n = 36?
Comprehension:
Direction: Based on the following information, answer the questions.
For an experiment, a sample of 25 observations from normal distribution with mean 98.6 and s.d. 17.2 was selected. Answer the following questions:
What is the standard error of mean?
If the standard deviation of 0, 1, 2, 3 ______ 9 is K, then the standard deviation of 10, 11, 12, 13 _____ 19 will be:
What is the standard deviation of the observations
−√6, −√5, −√4, −1, 1, √4, √5, √6?
If the mean of a frequency distribution is 100 and the coefficient of variation is 45%, then what is the value of the variance?
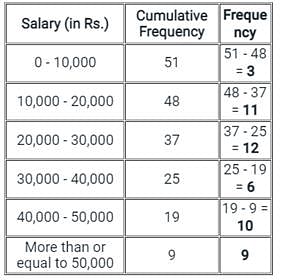
Consider the following distribution:
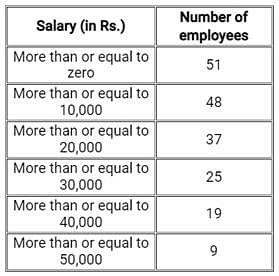
The frequency of class interval 30,000 - 40,000 is:
|
144 videos|100 docs|61 tests
|


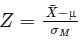 follows standard normal distribution.
follows standard normal distribution.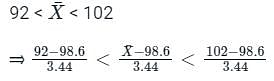


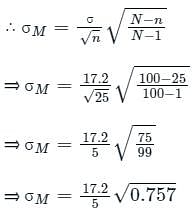
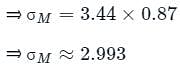

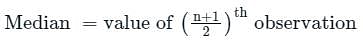


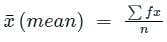
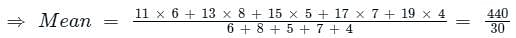
 follows standard normal distribution.
follows standard normal distribution.