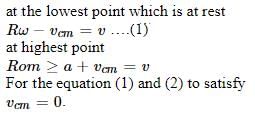All Courses
Get the App Signup / Login
Sign in Open App
JEE Exam  >  JEE Tests  >  Chapter-wise Tests for JEE Main & Advanced  >  Test: Rotational Motion (Competition Level 2) - JEE MCQ

Test: Rotational Motion (Competition Level 2) - JEE MCQ


Test Description

25 Questions MCQ Test Chapter-wise Tests for JEE Main & Advanced - Test: Rotational Motion (Competition Level 2)

Test: Rotational Motion (Competition Level 2) for JEE 2024 is part of Chapter-wise Tests for JEE Main & Advanced preparation. The Test: Rotational Motion (Competition Level 2) questions and answers have been prepared according to the JEE exam syllabus.The Test: Rotational Motion (Competition Level 2) MCQs are made for JEE 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Rotational Motion (Competition Level 2) below.
Solutions of Test: Rotational Motion (Competition Level 2) questions in English are available as part of our Chapter-wise Tests for JEE Main & Advanced for JEE & Test: Rotational Motion (Competition Level 2) solutions in Hindi for Chapter-wise Tests for JEE Main & Advanced course. Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free. Attempt Test: Rotational Motion (Competition Level 2) | 25 questions in 50 minutes | Mock test for JEE preparation | Free important questions MCQ to study Chapter-wise Tests for JEE Main & Advanced for JEE Exam | Download free PDF with solutions
*Multiple options can be correct
Test: Rotational Motion (Competition Level 2) - Question 1
Save

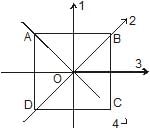
ABCD is a square plate with centre O. The moments of inertia of the plate about the perpendicular axis through O is I and about the axes 1, 2, 3 & 4 are I1, I2, I3 & I4 respectively. It follows that :

                              

Detailed Solution for Test: Rotational Motion (Competition Level 2) - Question 1

The perpendicular axis theorem states that the moment of inertia of a planar lamina about an axis perpendicular to the plane of the lamina is equal to the sum of the moments of inertia of the lamina about the two axes at right angles to each other, in its own plane intersecting each other at the point where the perpendicular axis passes through it.
Also as the given lamina is a square the axises through all the faces and all the diagonals are equal among themselves.

*Multiple options can be correct
Test: Rotational Motion (Competition Level 2) - Question 2
Save

A rod of weight w is supported by two parallel knife edges A and B and is in equilibrium in a horizontal position. The knives are at a distance d from each other. The centre of mass of the rod is at a distance x from A.

1 Crore+ students have signed up on EduRev. Have you? Download the App
*Multiple options can be correct
Test: Rotational Motion (Competition Level 2) - Question 3
Save

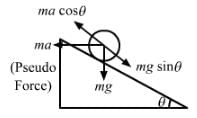
A block with a square base measuring axa and height h, is placed on an inclined plane. The coefficient of friction is m. The angle of inclination (q) of the plane is gradually increased. The block will

Detailed Solution for Test: Rotational Motion (Competition Level 2) - Question 3

For topping before sliding
From translational equilibrium
fl>mg sinθ
μmgcosθmgsinθ
μ>tanθ…(1)
taking rotation torque about N to topple
mgsinθ×(h/2)>mgcosθ×(a/2)⇒tanθ>(a/h) ….(2)
From (1) and (2) μ>a/h
For slide before toppling
for translatinal motion
mgsinθ>μmgcosθtanθ>μ ...(1)
mgcosθ×(a/2)>mgsinθ×(h/2)⇒2h>tanθ….(2)
From (1) and (2) (a/h)>μah>μ or μ<a/h.
 

*Multiple options can be correct
Test: Rotational Motion (Competition Level 2) - Question 4
Save

A body is in equilibrium under the influence of a number of forces. Each force has a different line of action. The minimum number of forces required is
Detailed Solution for Test: Rotational Motion (Competition Level 2) - Question 4

If they are not parallel then we can assume a case where they are inclined at 120o to each other and that will cover all scenarios
If they are parallel then assume two forces acting upwards F1 and F2 that will balance the net torque and F3 acting downwards to balance out the net force
For the final case of 4 forces it will be a special case of the previous scenario. Assume F1 and F2 acting downwards and F3 and F4 acting upwards.

*Multiple options can be correct
Test: Rotational Motion (Competition Level 2) - Question 5
Save

A block of mass m moves on a horizontal rough surface with initial velocity v. The height of the centre of mass of the block is h from the surface. Consider a point A on the surface
Detailed Solution for Test: Rotational Motion (Competition Level 2) - Question 5

The line of motion of the block passes through the center of mass and indicates the motion of center of mass. Hence, angular momentum about A is mvh initially. Since, the block is moving on a horizontal rough surface, due to  the frictional force the block will stop moving after some time. Hence, the velocity of the block decreases as time passes and due to this angular momentum is not conserved about A

*Multiple options can be correct
Test: Rotational Motion (Competition Level 2) - Question 6
Save

Four point masses are fastened to the corners of a frame of negligible mass lying in the xy plane. Let w be the angular speed of rotation. Then

                                    
Detailed Solution for Test: Rotational Motion (Competition Level 2) - Question 6


Ix=2M(0)+2m(b2)=2mb2
KEx=(1/2)Ix ω2=mb2ω2
Iy=2M(a2)+2m(0)=2Ma2
KEy=(1/2)Iyω2=Ma2ω2
Iz=2M(a2)+2m(b2)=2(Ma2+mb2)
KEz=(1/2)Izω2=(Ma2+mb2)ω2

*Multiple options can be correct
Test: Rotational Motion (Competition Level 2) - Question 7
Save

A particle falls freely near the surface of the earth. Consider a fixed point O (not vertically below the particle) on the ground.
*Multiple options can be correct
Test: Rotational Motion (Competition Level 2) - Question 8
Save

A man spinning in free space changes the shape of his body, eg. by spreading his arms or curling up. By doing this, he can change his
Detailed Solution for Test: Rotational Motion (Competition Level 2) - Question 8
  1. If size changes then obviously MOI changes
  2. By conservation of angular momentum it stays the same
  3. L = Iw, since L is constant then if I changes w has to change
  4. KE = L2/2I, to KE will also change
*Multiple options can be correct
Test: Rotational Motion (Competition Level 2) - Question 9
Save

A ring rolls without slipping on the ground. Its centre C moves with a constant speed u. P is any point on the ring. The speed of P with respect to the ground is v.
Detailed Solution for Test: Rotational Motion (Competition Level 2) - Question 9

The bottom point remains stationary at all times thereby having zero velocity.
Velocity at centre is v.
If the angular velocity is ω, and radius as R we have the velocity of the wheel at the top and bottom as-
vtop​=u+Rω and vbottom​=u−Rω
We know vbottom​ as zero giving u=Rω
Thus we have vtop​=2u
Thus we conclude that the velocity varies between 0 and 2u.
If CP is horizontal then we would have two components of the velocity, one is u in horizontal direction and the other is v=Rω in the vertical direction which is again equal to u. Thus, the resultant is √2​u.

*Multiple options can be correct
Test: Rotational Motion (Competition Level 2) - Question 10
Save

A disc of circumference s is at rest at a point A on a horizontal surface when a constant horizontal force begins to act on its centre. Between A and B there is sufficient friction to prevent slipping, and the surface is smooth to the right of B. AB = s. The disc moves from A to B in time T. To the right of B,

                          
Detailed Solution for Test: Rotational Motion (Competition Level 2) - Question 10
  1. This is wrong because the linear acceleration will increase
  2. By the previous argument this is correct
  3. No, it will complete one rotation in time T
  4. Since the acceleration will be greater the distance covered in the same time T will be greater than s
*Multiple options can be correct
Test: Rotational Motion (Competition Level 2) - Question 11
Save

In the figure shown, the plank is being pulled to the right with a constant speed v. If the cylinder does not slip then :

                                   
Detailed Solution for Test: Rotational Motion (Competition Level 2) - Question 11


So, Rw = v ⇒ w = v/R

*Multiple options can be correct
Test: Rotational Motion (Competition Level 2) - Question 12
Save

If a cylinder is rolling down the incline with sliding
Detailed Solution for Test: Rotational Motion (Competition Level 2) - Question 12

For sliding Vcm > Rw
If the rate of change of Vcm is greater than rate of change of angular velocity i.e. dVcm/dt > dw/dt then pure rolling will not happen
But if dVcm/dt < dw/dt then pure rolling may start

*Multiple options can be correct
Test: Rotational Motion (Competition Level 2) - Question 13
Save

Which of the following statements are correct
*Multiple options can be correct
Test: Rotational Motion (Competition Level 2) - Question 14
Save

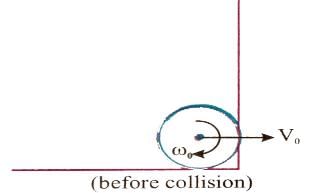
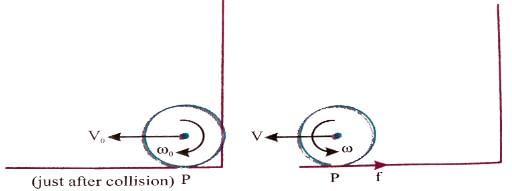
Consider a sphere of mass `m' radius `R' doing pure rolling motion on a rough surface having velocity  as shown in the Figure. It makes an elastic impact with the smooth wall and moves back and starts pure rolling after some time again.

                               
Detailed Solution for Test: Rotational Motion (Competition Level 2) - Question 14

Taking angular momentum about the point PP
Iω0−mV0R=Iω + mVR
⇒ (2/5)mR2×V0/R−mV0R=2/5mR2×V/R+mVR
⇒V=−3V0/7


 

*Multiple options can be correct
Test: Rotational Motion (Competition Level 2) - Question 15
Save

A solid sphere, a hollow sphere and a disc, all having same mass and radius, are placed at the top of an incline and released. The friction coefficients between the objects and the incline are same and not sufficient to allow pure rolling. The smallest kinetic energy at the bottom of the incline will be achieved by
Detailed Solution for Test: Rotational Motion (Competition Level 2) - Question 15

Using Newton’s second law of motion, we get
Mgsinθ – μMgcosθ = Ma
So, a = gsinθ – μgcosθ which means that acceleration is independent of mass and since s = ½ at2 so t is same.

*Multiple options can be correct
Test: Rotational Motion (Competition Level 2) - Question 16
Save

Fig. shows a smooth inclined plane fixed in a car accelerating on a horizontal road. The angle of incline q is related to the acceleration a of the car as a = g tan q. If the sphere is set in pure rotation on the incline.

                            
Detailed Solution for Test: Rotational Motion (Competition Level 2) - Question 16


From the free body diagram of sphere, we have:
Net force on the sphere along the incline,
 Fnet = mgsinθ − macosθ    …(i)
On putting a = gtanθ in equation (i), we get:
Fnet = 0
Therefore, if the sphere is set in pure rolling on the incline, it will continue pure rolling.
 

Test: Rotational Motion (Competition Level 2) - Question 17
Save

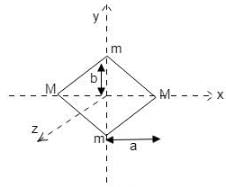
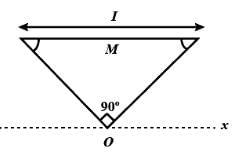
The figure shows an isosceles triangular plate of mass M and base L. The angle at the apex is 90°. The apex lies at the origin and the base is parallel to X - axis.

                                                                                                                                                                   The moment of inertia of the plate about the z-axis is
Detailed Solution for Test: Rotational Motion (Competition Level 2) - Question 17

By the perpendicular axis theorem, moment of inertia of z axis = moment of inertia of y axis + x axis
ml2/12 + ml2/12
ml2/6

Test: Rotational Motion (Competition Level 2) - Question 18
Save

The moment of inertia of the plate about the x-axis is
Detailed Solution for Test: Rotational Motion (Competition Level 2) - Question 18

Test: Rotational Motion (Competition Level 2) - Question 19
Save

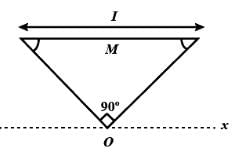
The moment of inertia of the plate about its base parallel to the x-axis is
Test: Rotational Motion (Competition Level 2) - Question 20
Save

The moment of inertia of the plate about the y-axis is
*Multiple options can be correct
Test: Rotational Motion (Competition Level 2) - Question 21
Save

A uniform rod is fixed to a rotating turntable so that its lower end is on the axis of the turntable and it makes an angle of 20° to the vertical. (The rod is thus rotating with uniform angular velocity about a vertical axis passing through one end.) If the turntable is rotating clockwise as seen from above.

                                                                                                                                                                         What is the direction of the rod's angular momentum vector (calculated about its lower end)
*Multiple options can be correct
Test: Rotational Motion (Competition Level 2) - Question 22
Save

Is there a torque acting on it, and if so in what direction?
Detailed Solution for Test: Rotational Motion (Competition Level 2) - Question 22

*Multiple options can be correct
Test: Rotational Motion (Competition Level 2) - Question 23
Save

A cylinder and a ring of same mass M and radius R are placed on the top of a rough inclined plane of inclination q. Both are released simultaneously from the same height h.

Choose the correct statement(s) related to the motion of each body
*Multiple options can be correct
Test: Rotational Motion (Competition Level 2) - Question 24
Save

Identify the correct statement(s)
Test: Rotational Motion (Competition Level 2) - Question 25
Save

When these bodies roll down to the foot of the inclined plane, then
446 docs|930 tests
Join Course
Information about Test: Rotational Motion (Competition Level 2) Page
In this test you can find the Exam questions for Test: Rotational Motion (Competition Level 2) solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Rotational Motion (Competition Level 2), EduRev gives you an ample number of Online tests for practice

Top Courses for JEE

Download as PDF

Top Courses for JEE

Important Questions for Rotational Motion (Competition Level 2)

Find all the important questions for Rotational Motion (Competition Level 2) at EduRev.Get fully prepared for Rotational Motion (Competition Level 2) with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Rotational Motion (Competition Level 2) syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Rotational Motion (Competition Level 2) resources.

Rotational Motion (Competition Level 2) MCQs with Answers

Prepare for the Rotational Motion (Competition Level 2) within the JEE exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Rotational Motion (Competition Level 2) Chapter-wise Tests for JEE Main & Advanced

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Rotational Motion (Competition Level 2) with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup